Blog de conocimiento gratuito: linux, programación, open source, bases de datos, android, frameworks, web e informática en general.
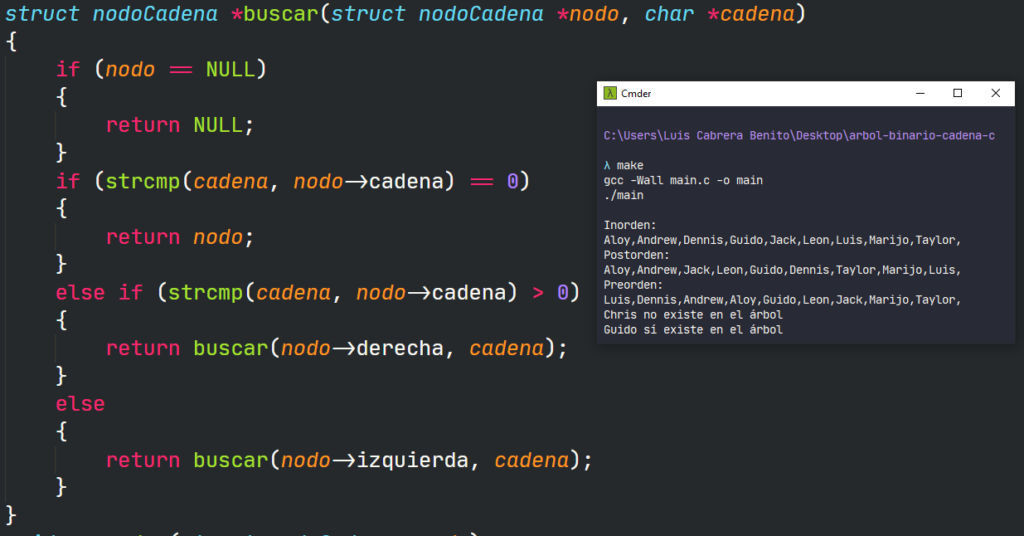
Ya te enseñé a implementar un árbol binario en Java, insertar elementos, recorrer de 3 maneras distintas y buscar un elemento pero no vimos cómo eliminar un elemento de ese ABB.
Por ello es que en este corto post de programación en Java vamos a ver cómo eliminar un nodo, hoja o dato de un árbol binario sin importar su posición y respetando a los nodos hijos en caso de que tenga.
Hoy vamos a ver cómo implementar el ordenamiento por mezcla o merge sort en Python. Básicamente este algoritmo nos va a servir para ordenar un arreglo de cualquier tipo (suponiendo que los valores son comparables).
Hay varios enfoques para este algoritmo; algunos usan una función y otros usan 2. Yo usaré éste último enfoque pues todo queda más claro.
Por cierto, también usaremos la recursividad, ya que es un aspecto clave al momento de ordenar un array con merge sort en Python.
En el post de hoy vamos a ver cómo ordenar un arreglo de C# (c sharp .NET) usando el algoritmo de Quicksort.
Vamos a hacer el algoritmo a mano, es decir, creando nuestras propias funciones para el ordenamiento de un array usando Quicksort o qs.
En este post de programación en Python te enseñaré a resolver un ejercicio sobre cómo saber si una palabra o frase es palíndroma o si es un palíndromo.
Se dice que una cadena es palíndroma cuando se lee igual de derecha a izquierda que de izquierda a derecha, quitando espacios y acentos.
Por ejemplo, si fuéramos estrictos, la frase “Isaac no ronca así “ no es un palíndromo por los acentos y espacios, pero si se los removemos queda como “isaacnoroncaasi” y esa string sí es un palíndromo.
Entonces vamos a ver un programa de Python que nos dirá si una cadena es o no palíndroma, opcionalmente removiendo los espacios y acentos. Además, vamos a ver dos enfoques: el recursivo y el que utiliza ciclos.
Hoy vamos a ver cómo obtener el máximo común divisor de dos números usando el lenguaje de programación Python.
Usaremos Python para escribir dos funciones que nos van a ayudar a calcular el MCD de dos números, una recursiva y otra usando el ciclo while.
Recuerda que el máximo común divisor de dos números es el entero máximo que puede dividir a dos números sin dejar residuo.
Por ejemplo, el máximo común divisor de 6 y 20 es 2, ya que no hay número mayor que pueda dividir a ambos números (ya que el 3 puede dividir al 6 pero no al 20).
Veamos cómo resolver este ejercicio de programación con Python a través del algoritmo de Euclides.
En este post te mostraré cómo implementar la estructura de datos de árbol binario en ANSI C en donde el dato de cada nodo o rama será una cadena.
Te enseñaré cómo agregar un struct de nodo de árbol cuyo dato es char*, elegir si el nodo va a la izquierda o derecha (comparando cadenas) , recorrer el árbol en preorden, inorden y postorden y también hacer una búsqueda en el mismo.
Me estoy basando en el tutorial de árboles binarios en C que presenté anteriormente, solo que en aquel entonces fue con un tipo de dato entero, ahora lo haré con strings.
Nota: nodo y rama serán usados como sinónimos a lo largo de este post.
En este post te mostraré cómo obtener el factorial de un número usando Python. Vamos a ver dos métodos: de manera iterativa con un ciclo, y de manera recursiva en donde la función se llama a sí misma.
Recuerda que el factorial de un número es el resultado de multiplicar ese número por todos los números que existen desde él hasta el 1. Por ejemplo, el factorial de 5 es 120 pues 5 * 4 * 3 * 2 * 1 es 120.
Voy a encerrar el comportamiento de este programa en funciones para su fácil reutilización. De hecho el método con recursión no puede estar en otro lugar más que en una función.
Hoy te enseñaré cómo trabajar con la secuencia Fibonacci en Python. Te enseñaré a obtener el número que va en determinada posición, así como imprimir toda la serie hasta determinado número.
Veremos las dos formas de trabajar con esta sucesión en Python: de manera iterativa con un ciclo for, y de manera recursiva invocando a la función dentro de sí misma.