En este post te mostraré cómo obtener pi o calcular pi usando la serie de Leibniz en el lenguaje de programación C. Si bien esto es para C, también puede funcionar para C++.

La serie de Leibniz dice que pi se puede obtener a partir de la siguiente sucesión: 4/1 – 4/3 + 4/5 – 4/7 + 4/9…

Si te fijas, el 4 (numerador) es fijo, y el denominador se aumenta en 2. Además, en cada paso se intercambia el signo.

Nota: este cálculo es, digamos, lento, además de que su precisión depende del número de iteraciones que se hagan. Solo sirve para estudiar cómo es su algoritmo y ponerlo como ejercicio de programación.

Tal vez tú solo quieras obtener y usar el valor de pi en C, para lo cual existen ya otros métodos.

El número de iteraciones

Como lo mencioné anteriormente, entre más iteraciones hagamos, más preciso será el cálculo. Con iteraciones me refiero a las operaciones de la serie que hagamos.

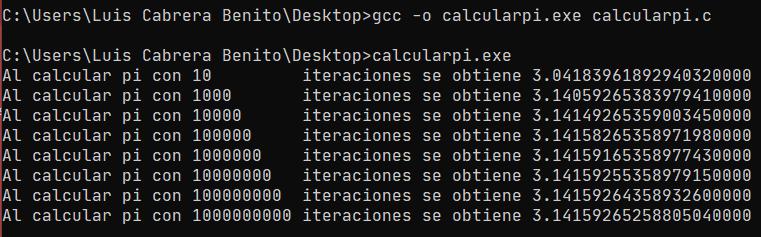
También es importante notar que a mayor número de iteraciones o pasos, más tiempo se lleva. En mi computadora el máximo que pude ejecutar en un tiempo razonable fue 1000000000 pasos.

Dicho esto, vamos a la función.

Función para calcular el pi en C usando serie de Leibniz

La función recibe el número de pasos que hay que dar y hace un ciclo for con todos esos pasos. Dentro de cada paso del ciclo se le va sumando a pi (inicialmente en 0) el valor de dividir 4 entre el denominador actual.

Además, se toma en cuenta el operador, pues recuerda que en cada paso se alterna de signo; para hacerlo simple podemos colocarlo en 1 y -1 para más tarde multiplicarlo.

Queda así:

/*
    Calcular pi usando la fórmula de Leibniz

    Recuerda: entre más iteraciones, mayor precisión

*/

double calcularPi(double iteraciones) {
  double numerador = 4;
  double denominador = 1; // A este lo vamos a ir aumentando de 2 en 2
  double pi = 0;
  int x = 0;
  // Recuerda que es alternar entre negativo y positivo; por eso la bandera.
  // Comenzamos en positivo
  int operador = 1;
  for (x; x < iteraciones; x++) {
    pi += operador * (numerador / denominador);
    denominador += 2; // El denominador aumenta de 2 en 2
    operador *= -1;   // Alternamos operador
  }
  return pi;
}

Para usarla la invocamos así:

double pi = calcularPi(iteraciones);

Veamos un ejemplo.

Calculando pi en C

En el método main podemos probar con ciertas iteraciones e imprimir los resultados para comprobar que realmente entre más pasos, mayor precisión.

El código completo queda así:

/*
  ____          _____               _ _           _       
 |  _ \        |  __ \             (_) |         | |      
 | |_) |_   _  | |__) |_ _ _ __ _____| |__  _   _| |_ ___ 
 |  _ <| | | | |  ___/ _` | '__|_  / | '_ \| | | | __/ _ \
 | |_) | |_| | | |  | (_| | |   / /| | |_) | |_| | ||  __/
 |____/ \__, | |_|   \__,_|_|  /___|_|_.__/ \__, |\__\___|
         __/ |                               __/ |        
        |___/                               |___/         
    
    Blog:       https://parzibyte.me/blog
    Ayuda:      https://parzibyte.me/blog/contrataciones-ayuda/
    Contacto:   https://parzibyte.me/blog/contacto/
    
    Copyright (c) 2020 Luis Cabrera Benito
    Licenciado bajo la licencia MIT
    
    El texto de arriba debe ser incluido en cualquier redistribución

*/
#include <stdio.h>  // Para printf
#include <stdlib.h> // Para EXIT_SUCCESS

/*
    Calcular pi usando la fórmula de Leibniz

    Recuerda: entre más iteraciones, mayor precisión

*/

double calcularPi(double iteraciones) {
  double numerador = 4;
  double denominador = 1; // A este lo vamos a ir aumentando de 2 en 2
  double pi = 0;
  int x = 0;
  // Recuerda que es alternar entre negativo y positivo; por eso la bandera.
  // Comenzamos en positivo
  int operador = 1;
  for (x; x < iteraciones; x++) {
    pi += operador * (numerador / denominador);
    denominador += 2; // El denominador aumenta de 2 en 2
    operador *= -1;   // Alternamos operador
  }
  return pi;
}

int main() {
  double iteraciones = 10;
  double pi = calcularPi(iteraciones);
  printf("Al calcular pi con %-10.lf iteraciones se obtiene %1.20lf\n",
         iteraciones, pi);
  iteraciones = 1000;
  pi = calcularPi(iteraciones);
  printf("Al calcular pi con %-10.lf iteraciones se obtiene %1.20lf\n",
         iteraciones, pi);
  iteraciones = 10000;
  pi = calcularPi(iteraciones);
  printf("Al calcular pi con %-10.lf iteraciones se obtiene %1.20lf\n",
         iteraciones, pi);
  iteraciones = 100000;
  pi = calcularPi(iteraciones);
  printf("Al calcular pi con %-10.lf iteraciones se obtiene %1.20lf\n",
         iteraciones, pi);
  iteraciones = 1000000;
  pi = calcularPi(iteraciones);
  printf("Al calcular pi con %-10.lf iteraciones se obtiene %1.20lf\n",
         iteraciones, pi);
  iteraciones = 10000000;
  pi = calcularPi(iteraciones);
  printf("Al calcular pi con %-10.lf iteraciones se obtiene %1.20lf\n",
         iteraciones, pi);
  iteraciones = 100000000;
  pi = calcularPi(iteraciones);
  printf("Al calcular pi con %-10.lf iteraciones se obtiene %1.20lf\n",
         iteraciones, pi);
  iteraciones = 1000000000;
  pi = calcularPi(iteraciones);
  printf("Al calcular pi con %-10.lf iteraciones se obtiene %1.20lf\n",
         iteraciones, pi);
}

Al ejecutarlo podemos ver cómo es que aumenta la precisión de Pi, que por cierto, recordemos que es un número infinito hasta la fecha (o algo así, no me vayan a mirar feo los matemáticos)