Hoy vamos a ver cómo implementar el método de Newton para encontrar aproximaciones de los ceros o raíces de una función real en C++.

Resolver derivada y ecuación

Primero necesitamos definir las funciones que resuelven la fórmula y la derivada. Quedan así:

A estas funciones las vamos a invocar para cada valor en un ciclo más tarde.

Método de Newton en C++

Después podemos implementar el método de Newton en CPP así:

Como puedes ver hacemos un ciclo infinito que se romperá solo cuando xi_xi sea 0. Además, estamos usando la función abs.

Dentro del ciclo también invocamos a resolverEcuacion y resolverDerivada para cada valor y lo vamos imprimiendo y alineando con printf.

En mi caso si lo ejecuto se ve así:

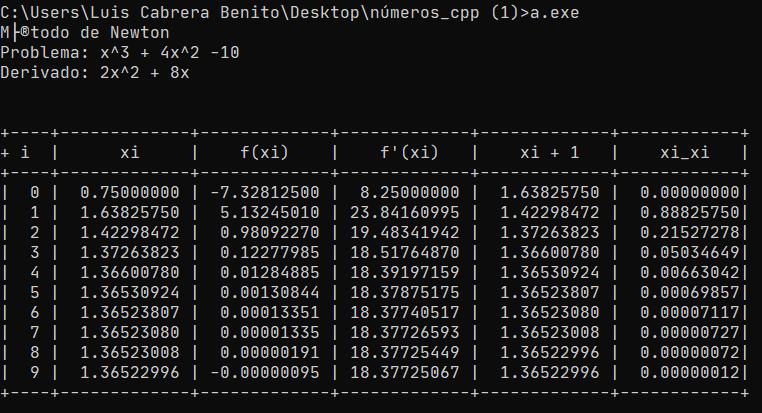
Solo hay un pequeño inconveniente con el acento, pero los datos son correctos.