En este post te mostraré cómo usar el método de la bisección en C++ para la búsqueda de raíces. Se imprimirá una tabla con todas las iteraciones hasta que el error sea mínimo.
Lo hice con una ecuación o fórmula que puede cambiarse según sea el caso.
Método de la bisección en C++
La verdad es que no soy un matemático, pero sí un programador. El código queda así:
/*
____ _____ _ _ _
| _ \ | __ \ (_) | | |
| |_) |_ _ | |__) |_ _ _ __ _____| |__ _ _| |_ ___
| _ <| | | | | ___/ _` | '__|_ / | '_ \| | | | __/ _ \
| |_) | |_| | | | | (_| | | / /| | |_) | |_| | || __/
|____/ \__, | |_| \__,_|_| /___|_|_.__/ \__, |\__\___|
__/ | __/ |
|___/ |___/
Blog: https://parzibyte.me/blog
Ayuda: https://parzibyte.me/blog/contrataciones-ayuda/
Contacto: https://parzibyte.me/blog/contacto/
Copyright (c) 2020 Luis Cabrera Benito
Licenciado bajo la licencia MIT
El texto de arriba debe ser incluido en cualquier redistribución
===========================================
Método de la bisección en C++
===========================================
*/#include<iostream>#include<cmath>usingnamespace std;floatresolverEcuacion(float valor){// Con la ecuación: X^3 + 4X ^2 -10returnpow(valor,3)+4*(pow(valor,2))-10;}intmain(){int iterador =1;/*
a = inferior
b = superior
*/float a =1;float b =2;float xi_xi =0;float ultimo_xi =0;printf("|-----------------------------------------------------------------------""--------------------------------------------\n");printf("| i | a | b | f(a) | f(b) | xi "" | f(xi) |f(a) * f(xi) | xi-xi_ |\n");printf("|-----------------------------------------------------------------------""--------------------------------------------\n");while(1){float fa =resolverEcuacion(a);float fb =resolverEcuacion(b);float xi =(a + b)/2;float fxi =resolverEcuacion(xi);float fa_fxi = fa * fxi;
xi_xi =abs(xi - ultimo_xi);printf("|%3d |%12.8f |%12.8f |%12.8f |%12.8f |%12.8f |%12.8f |%12.8f ""|%12.8f\n",
iterador, a, b, fa, fb, xi, fxi, fa_fxi, xi_xi);
iterador++;if(fa_fxi >0){
a = xi;}else{
b = xi;}
ultimo_xi = xi;if(xi_xi ==0){break;}}}
Presta atención a la función resolverEcuacion pues ahí puedes cambiar la fórmula. Recuerda que la tabla se imprimirá y que el ciclo infinito se romperá cuando xi_xi sea 0.
Aquí tienes el ejemplo de cómo se ejecuta:
Método de la bisección en C++
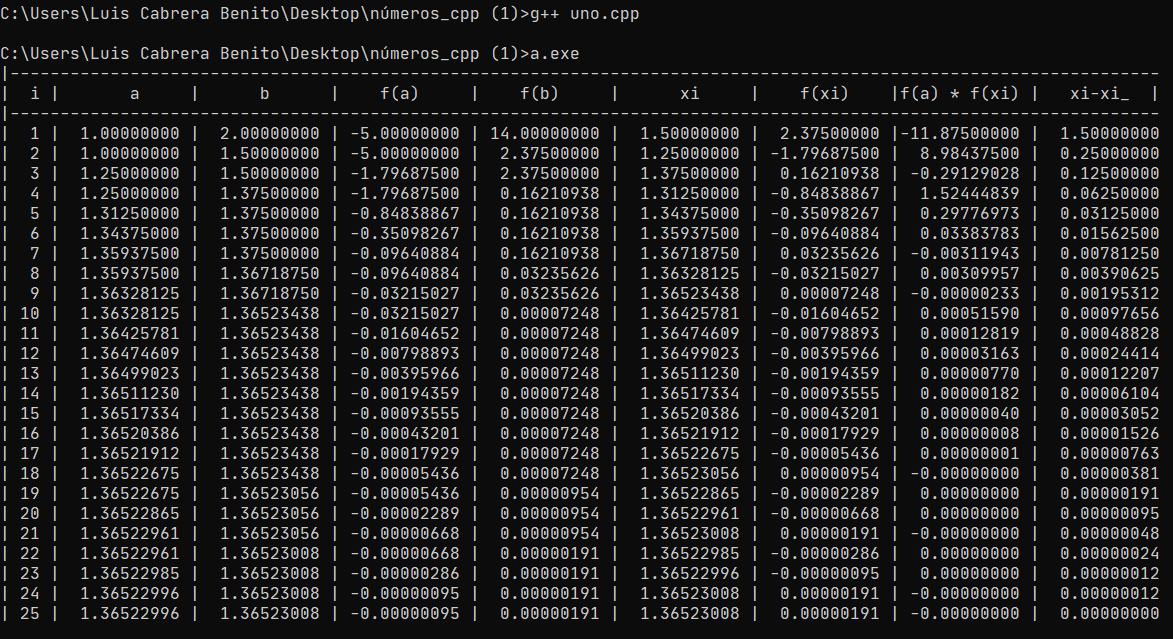
Nota: para alinear los valores e imprimir la tabla utilicé printf.
Estoy aquí para ayudarte
Estoy aquí para ayudarte en todo lo que necesites. Si requieres alguna modificación en lo presentado en este post, deseas asistencia con tu tarea, proyecto o precisas desarrollar un software a medida, no dudes en contactarme. Estoy comprometido a brindarte el apoyo necesario para que logres tus objetivos. Mi correo es parzibyte(arroba)gmail.com, estoy como@parzibyte en Telegram o en mi página de contacto
No te pierdas ninguno de mis posts
Suscríbete a mi canal de Telegram para recibir una notificación cuando escriba un nuevo tutorial de programación.
Hoy vamos a ver cómo implementar el método de Newton para encontrar aproximaciones de los ceros o raíces de una función real en C++. Resolver derivada y ecuación Primero necesitamos definir las funciones que resuelven la fórmula y la derivada. Quedan así: float resolverEcuacion(float valor) { // Con la ecuación:…
Hoy veremos cómo implementar el método de la regla falsa en C++. Este método involucra el resolver la fórmula, obtener xr, definir los intervalos y buscar el valor deseado hasta que la tolerancia sea menor a la deseada. Funciones que resuelven la ecuación Primero veamos las funciones: double resolverEcuacion(double valor)…
Hoy veremos cómo es que, en Java, se pasan los parámetros a las funciones. Es decir, ¿En Java los parámetros se pasan por referencia o por valor? vamos a comprobarlo y explicarlo con este post. De entrada te digo que depende del tipo de dato y que, en términos simples,…
