Hoy vamos a ver cómo implementar el método de Newton para encontrar aproximaciones de los ceros o raíces de una función real en C++.

Resolver derivada y ecuación

Primero necesitamos definir las funciones que resuelven la fórmula y la derivada. Quedan así:

float resolverEcuacion(float valor) {
  // Con la ecuación: x^3 + 4x^2 -10
  return pow(valor, 3) + 4 * pow(valor, 2) - 10;
}

float resolverDerivada(float valor) {
  // Con la ecuación: 2x^2 + 8x
  return pow((2 * valor), 2) + 8 * valor;
}

A estas funciones las vamos a invocar para cada valor en un ciclo más tarde.

Método de Newton en C++

Después podemos implementar el método de Newton en CPP así:

/*
  ____          _____               _ _           _       
 |  _ \        |  __ \             (_) |         | |      
 | |_) |_   _  | |__) |_ _ _ __ _____| |__  _   _| |_ ___ 
 |  _ <| | | | |  ___/ _` | '__|_  / | '_ \| | | | __/ _ \
 | |_) | |_| | | |  | (_| | |   / /| | |_) | |_| | ||  __/
 |____/ \__, | |_|   \__,_|_|  /___|_|_.__/ \__, |\__\___|
         __/ |                               __/ |        
        |___/                               |___/         
    
    Blog:       https://parzibyte.me/blog
    Ayuda:      https://parzibyte.me/blog/contrataciones-ayuda/
    Contacto:   https://parzibyte.me/blog/contacto/
    
    Copyright (c) 2020 Luis Cabrera Benito
    Licenciado bajo la licencia MIT
    
    El texto de arriba debe ser incluido en cualquier redistribución

    ===========================================
    Método de Newton en C++
    ===========================================
*/#include <cmath>
#include <iostream>

using namespace std;

float resolverEcuacion(float valor) {
  // Con la ecuación: x^3 + 4x^2 -10
  return pow(valor, 3) + 4 * pow(valor, 2) - 10;
}

float resolverDerivada(float valor) {
  // Con la ecuación: 2x^2 + 8x
  return pow((2 * valor), 2) + 8 * valor;
}

int main() {
  int iterador = 0;
  float xi = 0.75;
  float xi_xi = 0;
  float ultimo_xi = 0;
  printf("Método de Newton\n");
  printf("Problema: x^3 + 4x^2 -10\n");
  printf("Derivado: 2x^2 + 8x\n\n\n");
  printf("+----+-------------+-------------+-------------+-------------+-------"
         "-----+\n");
  printf("+ i  |      xi     |    f(xi)    |    f'(xi)   |    xi + 1   |    "
         "xi_xi   |\n");
  printf("+----+-------------+-------------+-------------+-------------+-------"
         "-----+\n");
  while (1) {
    float fxi = resolverEcuacion(xi);
    float _fxi = resolverDerivada(xi);
    float xi_1 = xi - (fxi / _fxi);
    printf("|%3d |%12.8f |%12.8f |%12.8f |%12.8f |%12.8f|\n", iterador, xi, fxi,
           _fxi, xi_1, xi_xi);
    iterador++;
    ultimo_xi = xi;
    xi = xi_1;
    xi_xi = abs(xi - ultimo_xi);
    if (xi_xi == 0) {
      printf("+----+-------------+-------------+-------------+-------------+---"
             "---------+\n");
      break;
    }
  }
}

Como puedes ver hacemos un ciclo infinito que se romperá solo cuando xi_xi sea 0. Además, estamos usando la función abs.

Dentro del ciclo también invocamos a resolverEcuacion y resolverDerivada para cada valor y lo vamos imprimiendo y alineando con printf.

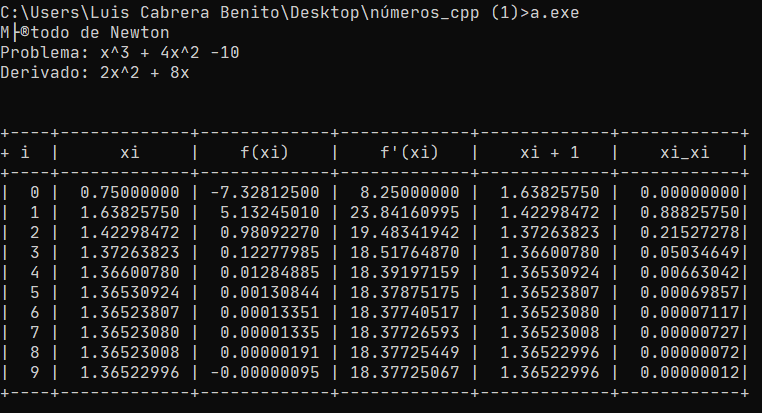
En mi caso si lo ejecuto se ve así:

Solo hay un pequeño inconveniente con el acento, pero los datos son correctos.