El día de hoy voy a explicar el algoritmo Raster bit image, mismo que es un método para convertir una imagen en bytes entendibles para el protocolo ESC POS de las impresoras térmicas.

Además de este algoritmo existen el Bit image column format, NV Graphics y otros de los que todavía no tengo conocimiento.

Estos 3 son los algoritmos más comunes a la hora de imprimir imágenes en una impresora térmica, si los conoces entonces no tendrás problemas al momento de imprimir imágenes en una impresora térmica.

Bien, veamos este último algoritmo que es realmente sencillo después de haber revisado los otros 2. Su comando es GS v 0 y recibe los bytes de la imagen en formato de raster.

Nota importante: recomiendo encarecidamente revisar los otros dos algoritmos, pues si bien todos son distintos, revisarlos te ayudará a entender la conversión de números, anchos, altos, bytes, LSB, MSB, etcétera.

Comando ESC POS GS v 0

El método de impresión de imágenes Raster bit image de las impresoras térmicas se define como:

GS v 0 m xL xH yL yH d1...dk

En este caso GS (Group separator), v y 0 son los bytes literales, esos bytes nunca cambian y son básicamente el inicio del comando. Veamos la definición de las otras variables.

La densidad: m

El parámetro m indica la densidad y básicamente permite alargar cada punto de la imagen impresa en la POS printer. Su valor (en decimal) puede ser 0, 1, 2, 3, 48, 49, 50 o 51.

1. Para imprimir la imagen en tamaño normal, hay que especificar 0 o 48
2. Si quieres que cada pixel de la imagen se alargue horizontalmente, hay que especificar 1 o 49
3. Por otro lado, si quieres que cada pixel se alargue verticalmente, especifica 2 o 50
4. Finalmente, para estirar la imagen tanto en el ancho como en el alto, especifica 3 o 51.

Ancho en bytes: x

Le toca el turno a los parámetros xL y xH. Recuerda que la L es de Low y la H de High, básicamente es para separar el valor de x en 2 bytes.

Para sacar la parte baja hay que calcular el residuo de dividir x entre 256, lo que en algunos lenguajes de programación se puede hacer con la operación módulo.

En el caso de la parte alta (High) hay que calcular el cociente de dividir x entre 256, lo que en algunos lenguajes equivale a dividir x entre 256 y redondear su valor al entero anterior más próximo.

Si te preguntas por el número 256, recuerda que es la cantidad de números que puedes representar con un byte de 8 bits, incluyendo al cero. Con dos bytes puedes representar hasta 65536 números, siendo el 65535 el más grande.

Calculando bytes a partir del ancho

Anteriormente te dije que debemos separar x en su parte alta y baja, lo cual ya hicimos; pero no hemos sacado el valor de x.

Básicamente este valor es la cantidad de bytes necesarios para representar una fila de pixeles a partir de nuestra imagen.

Recuerda que un byte tiene 8 bits, y como podemos representar un pixel por bit, caben 8 pixeles de imagen en un byte. Así que, suponiendo que el ancho de la imagen es múltiplo de 8 y que la cantidad de bits en un byte es igualmente 8, el ancho en bytes será igual a dividir el ancho entre 8.

Si el ancho de la imagen no es divisible entre 8 tienes que hacer los ajustes y operaciones necesarias como rellenar los bytes y redondear al siguiente entero más próximo.

El alto: y, yL y yH

Por otro lado también debemos enviar el alto de la imagen pero ahora solo el alto, sin calcular los bytes. La parte alta y baja se calculan igual, es decir:

• yL = y módulo 256
• yH = redondear hacia abajo el resultado de dividir y / 256

Los bytes: d1…dk

Finalmente podemos enviar los bytes de la imagen. Recuerda que en un byte caben 8 pixeles de la imagen. Cuando llenes un byte, agrega ese byte a una fila de bytes.

Los primeros 8 pixeles serán d1, los siguientes 8 pixeles serán d2, así hasta llegar a dk.

Para convertir la imagen a bytes ESC POS raster bit image sigue los siguientes pasos:

1. Recorre la imagen comenzando en 0,0 y avanza hasta ancho,0. Cuando llegues a ancho,0, avanza y en 1 de manera que ahora vas a recorrer desde 0,1 hasta ancho,1. Repite ese proceso hasta llegar al alto de la imagen (es decir, hasta ancho,alto).
2. Dicho con otras palabras, debes recorrer la imagen desde la esquina superior izquierda fila por fila de pixeles, bajando cada vez que completes una fila, hasta llegar a la parte baja de la imagen.
3. En cada paso del recorrido, decide si el pixel actual va a ser un 1 o un 0; para ello aplica el algoritmo que prefieras para convertir un RGBA a un uno o cero.
4. Agrega ese 1 o 0 al byte (comenzando por el MSB) y cuando el byte esté completo agrega ese byte al arreglo de bytes

Sigue el proceso hasta terminar de recorrer la imagen. Al final tendrás una colección de bytes que representan a d1 hasta dk.

Ejemplo real

Veamos un ejemplo de conversión de una imagen PNG a bytes ESC POS usando el método Raster bit image. La imagen presentada a continuación es la más pequeña que se puede imprimir usando este método, sin rellenar bytes.

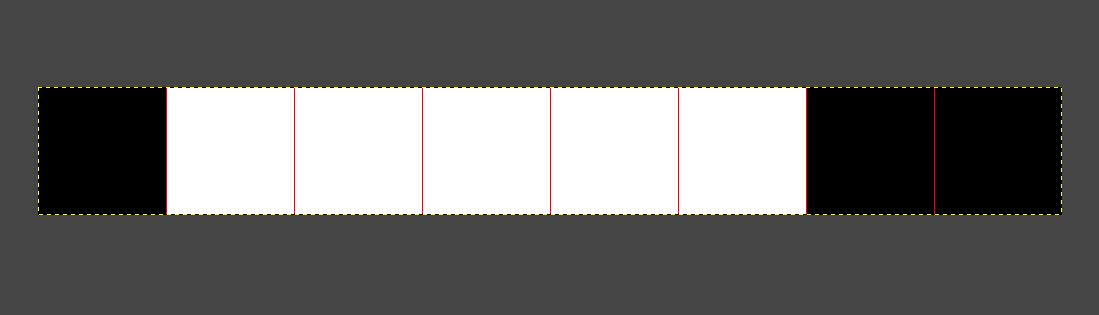
Le he hecho zoom y configurado la cuadrícula en el editor GIMP. La imagen que ves mide 8×1 y solo tiene 8 pixeles que son blancos o negros por simplicidad.

Primero vamos a calcular el byte de la imagen, si lo vemos en binario es 10000011, lo que equivale al valor 131 en decimal y 0x83 en hexadecimal.

Si la imagen midiera, por ejemplo, 16x1, necesitaríamos 2 bytes y cada byte estaría compuesto de un bit cuyo valor dependería del color del pixel.

Ya hicimos el cálculo de los bytes de la imagen, pero ahora comencemos viendo el comando desde el principio. Recuerda que es: GS v 0 m xL xH yL yH d1...dk

Primero colocaremos GS v 0, esos valores son literales. Para el caso de m voy a elegir un tamaño normal así que lo dejaré en 0. Nuestro comando en hexadecimal se ve así:

0x1d, 0x76 ,0x30 ,0x00

Para el caso de xL y xH primero calculamos el valor de x, que sería (ancho/8), lo que resulta en 1 ya que 8/8=1.

La parte baja se queda en 0x01, ya que 1%256=1, y la parte alta en 0x00 porque 1/256 es 0.00390625 pero redondeado hacia abajo es 0.

Luego calculamos el valor de yL y yH que se obtiene calculando la parte baja y alta de y. Recuerda que y es el alto de la imagen, así que en este caso equivale a 1. Entonces, yL es 0x01 y yH es 0x00.

Nuestro comando iba así: 0x1d, 0x76 ,0x30 ,0x00

Agregamos xL, xH, yL, yH que son: 0x01,0x00,0x01,0x00

Y queda así: 0x1d, 0x76 ,0x30 ,0x00, 0x01,0x00,0x01,0x00

Ya solo falta agregar los bytes de la imagen que son 0x83, así que en conjunto queda así:

0x1d, 0x76 ,0x30 ,0x00, 0x01,0x00,0x01,0x00, 0x83

Si nosotros enviamos esos bytes a una impresora térmica, se va a imprimir una imagen de 8×1 con una densidad normal. Obviamente no se va a ver porque es muy pequeña, pero con estas bases ya podemos imprimir cualquier imagen.

Otro ejemplo

Puede que el ejemplo anterior para convertir una imagen a bytes ESC POS con el método de rasterización no te haya quedado claro.

A continuación te muestro otro ejemplo con una imagen de 24×3, solo toma en cuenta que he utilizado imágenes que solo tienen conjuntos de pixeles negros o blancos por simplicidad, pero en una imagen real esto va a cambiar.

Siguiendo el algoritmo presentado anteriormente, la primera fila es 11111111, 00000000, 11111111 que en hexadecimal es 0xFF, 0x00, 0xFF.

Para la segunda fila empezamos en 0x00, luego 0xFF y finalmente 0x00.

En la última fila es 0xFF, 0x00 pero para el último grupo de 8 pixeles tenemos el valor 11111110 que es 254 en decimal y 0xFE en hexadecimal.

Por lo tanto, los bytes completos de la imagen son:

0xFF,0x00,0xFF,0x00,0xFF,0x00,0xFF,0x00,0xFE

Ahora solo resta calcular el encabezado y los otros valores. Para no hacer el artículo tan largo, te dejo los comandos ESC POS a continuación y dejaré que tú encuentres de dónde salen los valores siguiendo el tutorial:

0x1D, 0x76, 0x30, 0x00, 0x03, 0x00, 0x03, 0x00, 0xFF, 0x00, 0xFF, 0x00, 0xFF, 0x00, 0xFF, 0x00, 0xFE

Recuerda que ya tengo implementado este algoritmo en mi plugin para impresoras térmicas multiplataforma que puedes usar en conjunto con mi diseñador de recibos térmicos.