En el post de hoy vamos a ver cómo ordenar un arreglo de C# (c sharp .NET) usando el algoritmo de Quicksort.

Vamos a hacer el algoritmo a mano, es decir, creando nuestras propias funciones para el ordenamiento de un array usando Quicksort o qs.

El algoritmo

Para ordenar un arreglo usando quicksort aplicamos el método de divide y vencerás. Tendremos dos apuntadores al arreglo, uno a la izquierda y uno a la derecha (o uno al inicio y otro al final).

El lugar en donde el algoritmo se divide es en el método de la partición. Este método debe indicar en qué índice del arreglo debemos hacer la división, es decir, en cuál índice separar el arreglo en 2.

Dentro del algoritmo de la partición vamos acercando los extremos mientras que cada elemento del arreglo esté ordenado. Si encontramos que hay un elemento que no está ordenado entonces intercambiamos los valores de los dos extremos.

La partición se detiene y regresa cuando hemos acercado los extremos de tal modo que la izquierda es mayor o igual a la derecha. En ese punto devolvemos el índice de la derecha, mismo que será usado para hacer otras particiones.

Al final vamos a ir dividiendo el arreglo en partes más pequeñas, y ordenando a las mismas. Pero el verdadero ordenamiento viene en la partición.

Yo sé que es mucha explicación y que puede ser confusa, pero verás que en el código se entiende de mejor manera.

Quicksort en C#

Entonces debemos implementar dos funciones en C sharp. La primera va a ser quien se encargue de ir dividiendo el arreglo eligiendo la partición, invocando a la función dentro de sí misma usando recursión.

La segunda función es la de la partición, misma que se va a encargar de ordenar el arreglo y devolver el índice en donde se quedó.

Partición

Veamos la función de C# que se encarga de ordenar la porción del arreglo:

static int particion(int[] arreglo, int izquierda, int derecha)
{
    int pivote = arreglo[izquierda];
    while (true)
    {
        /*
        Acercar los extremos hacia el centro mientras se encuentren elementos ordenados
         */        while (arreglo[izquierda] < pivote)
        {
            izquierda++;
        }

        while (arreglo[derecha] > pivote)
        {
            derecha--;
        }
        // Si los extremos se cruzaron o superaron, entonces toda la porción del arreglo estaba ordenada
        if (izquierda >= derecha)
        {
            // Regresamos el índice para indicar hasta qué posición el arreglo está en orden
            return derecha;
        }
        else
        {
            // Si no estuvieron ordenados, vamos a hacer el intercambio
            int temporal = arreglo[izquierda];
            arreglo[izquierda] = arreglo[derecha];
            arreglo[derecha] = temporal;
            // Y acercamos en 1 los extremos
            derecha--; izquierda++;

        }
        // El while se repite hasta que izquierda >= derecha
    }
}

Como puedes notar, el código se explica por sí mismo apoyándose de los comentarios. Recuerda que el verdadero orden e intercambio está en la línea 27 en caso de que los elementos no hayan estado ordenados.

Función de qs

Y ahora que ya vimos la función de partición para elegir el pivote veamos la función quicksort para aplicar el algoritmo del mismo nombre en C#:

static void quicksort(int[] arreglo, int izquierda, int derecha)
{
    if (izquierda < derecha)
    {
        int indiceParticion = particion(arreglo, izquierda, derecha);
        quicksort(arreglo, izquierda, indiceParticion);
        quicksort(arreglo, indiceParticion + 1, derecha);
    }
}

Recuerda que aquí lo que se hace es ir dividiendo el arreglo. La primera parte es desde la izquierda hasta el pivote, y la segunda es desde el pivote + 1 hasta la derecha.

Conforme esta función se vaya invocando se va a ir partiendo al arreglo en trozos más pequeños.

Poniendo todo junto

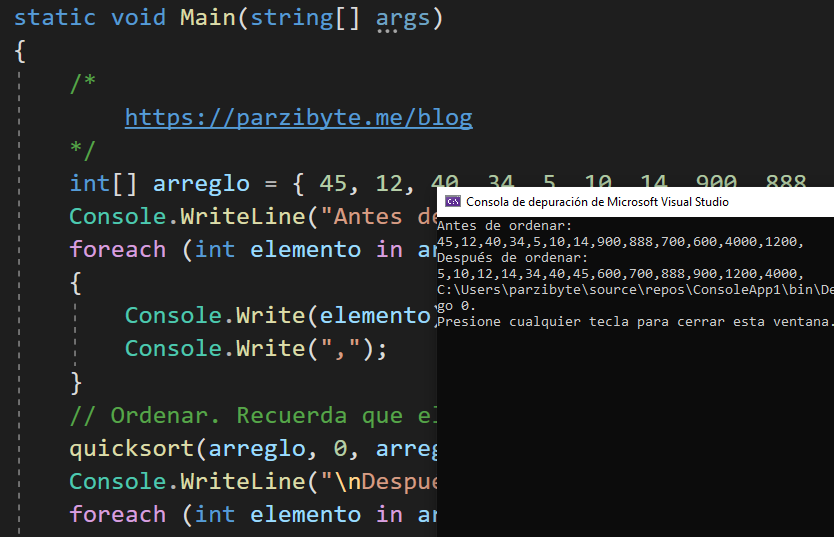
Es momento de ver el código completo con un ejemplo. El mismo queda como se ve a continuación. Presta atención al modo de uso que está dentro del método Main.

using System;

namespace ConsoleApp1
{
    class Program
    {
        static void quicksort(int[] arreglo, int izquierda, int derecha)
        {
            if (izquierda < derecha)
            {
                int indiceParticion = particion(arreglo, izquierda, derecha);
                quicksort(arreglo, izquierda, indiceParticion);
                quicksort(arreglo, indiceParticion + 1, derecha);
            }
        }
        static int particion(int[] arreglo, int izquierda, int derecha)
        {
            int pivote = arreglo[izquierda];
            while (true)
            {
                /*
                Acercar los extremos hacia el centro mientras se encuentren elementos ordenados
                 */                while (arreglo[izquierda] < pivote)
                {
                    izquierda++;
                }

                while (arreglo[derecha] > pivote)
                {
                    derecha--;
                }
                // Si los extremos se cruzaron o superaron, entonces toda la porción del arreglo estaba ordenada
                if (izquierda >= derecha)
                {
                    // Regresamos el índice para indicar hasta qué posición el arreglo está en orden
                    return derecha;
                }
                else
                {
                    // Si no estuvieron ordenados, vamos a hacer el intercambio
                    int temporal = arreglo[izquierda];
                    arreglo[izquierda] = arreglo[derecha];
                    arreglo[derecha] = temporal;
                    // Y acercamos en 1 los extremos
                    derecha--; izquierda++;

                }
                // El while se repite hasta que izquierda >= derecha
            }
        }
        static void Main(string[] args)
        {
            /*
                https://parzibyte.me/blog
            */            int[] arreglo = { 45, 12, 40, 34, 5, 10, 14, 900, 888, 700, 600, 4000, 1200 };
            Console.WriteLine("Antes de ordenar: ");
            foreach (int elemento in arreglo)
            {
                Console.Write(elemento);
                Console.Write(",");
            }
            // Ordenar. Recuerda que el arreglo original será modificado
            quicksort(arreglo, 0, arreglo.Length - 1);
            Console.WriteLine("\nDespués de ordenar: ");
            foreach (int elemento in arreglo)
            {
                Console.Write(elemento);
                Console.Write(",");
            }

        }

    }
}

Por cierto, en este caso he utilizado un arreglo de tipo entero pero puedes usar uno de cualquier tipo, por ejemplo uno de tipo string. Solo recuerda comparar correctamente los datos, ya que en el caso de las cadenas se usa CompareTo.

La salida ya la pudiste ver junto con el encabezado. Al final el arreglo estará ordenado usando el algoritmo quicksort.

Por aquí te dejo con más posts de C#.