Hoy vamos a ver cómo aplicar la búsqueda binaria para buscar elementos en arreglos usando el lenguaje de programación C# también conocido como C sharp.
Te voy a mostrar dos métodos: uno para hacer la búsqueda binaria (divide y vencerás) usando recursividad y otro método usando el ciclo while.
Al final tendremos dos funciones que nos permitirán buscar un elemento en un array usando el algoritmo de la búsqueda binaria.
Sobre la búsqueda binaria
Recuerda que el arreglo al que vamos a aplicar esta búsqueda (contrario a la búsqueda secuencial en donde no importa) debe estar ordenado.
Esta búsqueda utiliza el enfoque de divide y vencerás. Primero tomamos el elemento central que está entre nuestros límites y comparamos para ver si es lo que buscamos, en caso de que sí, regresamos el índice.
En caso de no encontrarlo entonces comparamos si el elemento central es menor o mayor al que buscamos. Si es menor entonces dividimos el arreglo desde el centro a la izquierda, y si es mayor, lo dividimos desde el centro a la derecha.
Esto ya lo expliqué más a fondo en un post dedicado a ello. Si te interesa profundizar, léelo aquí.
Búsqueda binaria en C# con recursión
Veamos el primer método de este programa en C# aplicando la recursividad. Vamos a implementar la búsqueda binaria, para ello necesitamos definir una función que recibirá:
- El arreglo
- La búsqueda
- El índice izquierdo
- El índice derecho
Y queda así:
static int busquedaBinaria(int[] arreglo, int busqueda, int izquierda, int derecha)
{
if (izquierda > derecha)
{
return -1;
}
// Comprobar si está en el centro
int indiceCentral = Convert.ToInt32(Math.Floor(Convert.ToDouble(izquierda + derecha) / 2));
int valorCentral = arreglo[indiceCentral];
if (valorCentral == busqueda)
{
return indiceCentral;
}
// Si no, debido a que esto ya está ordenado, analizamos dónde podría estar
if (busqueda < valorCentral)
{
// Si lo que buscamos es menor, debe estar a la izquierda
derecha = indiceCentral - 1;
}
else
{
// Si no, está a la derecha
izquierda = indiceCentral + 1;
}
return busquedaBinaria(arreglo, busqueda, izquierda, derecha);
}La condición de salida es que la izquierda supere a la derecha, ya que en ese caso habremos acabado de recorrer el arreglo; lo que significa que el elemento buscado no existe.
Después de eso hacemos la comparación. La aplicación del Divide y vencerás está en la línea 19 y línea 24, pues modificamos los límites y volvemos a invocar a la función (aplicando recursión).
La función nos va a devolver -1 o el índice del arreglo en donde se encuentra el elemento buscado.
Nota: en los modos de uso te enseñaré cómo invocar a la función por primera vez.
Búsqueda binaria con ciclo while en C#
Ahora veamos el enfoque con ciclos o loops. Básicamente es el mismo algoritmo en donde modificamos los límites pero ahora lo hacemos dentro del ciclo. Queda así:
static int busquedaBinariaWhile(int[] arreglo, int busqueda)
{
int izquierda = 0, derecha = arreglo.Length - 1;
while (izquierda <= derecha)
{
int indiceCentral = Convert.ToInt32(Math.Floor(Convert.ToDouble(izquierda + derecha) / 2));
int valorCentral = arreglo[indiceCentral];
// Si lo encontramos entonces regresamos el valor de manera inmediata
if (valorCentral == busqueda)
{
return indiceCentral;
}
// Si no, debido a que esto ya está ordenado, analizamos dónde podría estar
if (busqueda < valorCentral)
{
// Si lo que buscamos es menor, debe estar a la izquierda
derecha = indiceCentral - 1;
}
else
{
// Si no, está a la derecha
izquierda = indiceCentral + 1;
}
}
// Terminamos de buscar y no encontramos el elemento
return -1;
}Fíjate que en este caso la función no recibe la izquierda y derecha, pues no los necesitamos porque no vamos a volver a invocar a la función dentro de sí misma.
Modo de uso
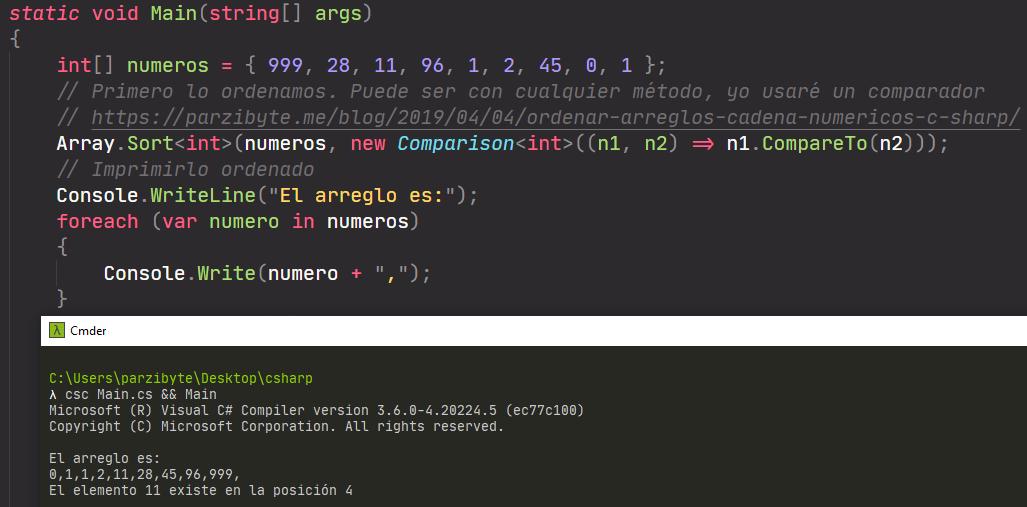
Ya te mostré las dos funciones. Esto fue con enteros pero igualmente funcionaría con cadenas, solo hay que comparar correctamente.
En fin, el modo de uso es el siguiente:
static void Main(string[] args)
{
int[] numeros = { 999, 28, 11, 96, 1, 2, 45, 0, 1 };
// Primero lo ordenamos. Puede ser con cualquier método, yo usaré un comparador
// https://parzibyte.me/blog/2019/04/04/ordenar-arreglos-cadena-numericos-c-sharp/
Array.Sort<int>(numeros, new Comparison<int>((n1, n2) => n1.CompareTo(n2)));
// Imprimirlo ordenado
Console.WriteLine("El arreglo es:");
foreach (var numero in numeros)
{
Console.Write(numero + ",");
}
Console.WriteLine("");
// Ahora sí, buscar de manera binaria
int busqueda = 11;
int indice = busquedaBinaria(numeros, busqueda, 0, numeros.Length - 1);
// Con while sería:
// int indice = busquedaBinariaWhile(numeros, busqueda);
if (indice == -1)
{
Console.WriteLine("La búsqueda no existe");
}
else
{
Console.WriteLine("El elemento {0} existe en la posición {1}", busqueda, indice);
}
}En la línea 3 declaro mi arreglo, después lo ordeno en la línea 6. Obviamente tú puedes usar cualquier método para ordenarlo, yo he usado ese por simplicidad.
Después en la línea 7 imprimo el arreglo para mostrar su estructura. Finalmente invoco a la función de búsqueda binaria en la línea 16, misma que me va a devolver un índice.
Nota: en el ejemplo estoy invocando a busquedaBinaria pero igualmente podrías invocar a busquedaBinariaWhile como se indica en el comentario. Fíjate que al inicio los límites del arreglo son 0 para la izquierda y la longitud del arreglo menos uno para la derecha.
Finalmente imprimo si el elemento fue encontrado o no, así como la posición del mismo.
Poniendo todo junto
El código completo en mi caso (por si quieres verlo todo) queda así:
using System;
namespace App
{
class Programa
{
static int busquedaBinaria(int[] arreglo, int busqueda, int izquierda, int derecha)
{
if (izquierda > derecha)
{
return -1;
}
// Comprobar si está en el centro
int indiceCentral = Convert.ToInt32(Math.Floor(Convert.ToDouble(izquierda + derecha) / 2));
int valorCentral = arreglo[indiceCentral];
if (valorCentral == busqueda)
{
return indiceCentral;
}
// Si no, debido a que esto ya está ordenado, analizamos dónde podría estar
if (busqueda < valorCentral)
{
// Si lo que buscamos es menor, debe estar a la izquierda
derecha = indiceCentral - 1;
}
else
{
// Si no, está a la derecha
izquierda = indiceCentral + 1;
}
return busquedaBinaria(arreglo, busqueda, izquierda, derecha);
}
static int busquedaBinariaWhile(int[] arreglo, int busqueda)
{
int izquierda = 0, derecha = arreglo.Length - 1;
while (izquierda <= derecha)
{
int indiceCentral = Convert.ToInt32(Math.Floor(Convert.ToDouble(izquierda + derecha) / 2));
int valorCentral = arreglo[indiceCentral];
// Si lo encontramos entonces regresamos el valor de manera inmediata
if (valorCentral == busqueda)
{
return indiceCentral;
}
// Si no, debido a que esto ya está ordenado, analizamos dónde podría estar
if (busqueda < valorCentral)
{
// Si lo que buscamos es menor, debe estar a la izquierda
derecha = indiceCentral - 1;
}
else
{
// Si no, está a la derecha
izquierda = indiceCentral + 1;
}
}
// Terminamos de buscar y no encontramos el elemento
return -1;
}
/*
https://parzibyte.me/blog
*/
static void Main(string[] args)
{
int[] numeros = { 999, 28, 11, 96, 1, 2, 45, 0, 1 };
// Primero lo ordenamos. Puede ser con cualquier método, yo usaré un comparador
// https://parzibyte.me/blog/2019/04/04/ordenar-arreglos-cadena-numericos-c-sharp/
Array.Sort<int>(numeros, new Comparison<int>((n1, n2) => n1.CompareTo(n2)));
// Imprimirlo ordenado
Console.WriteLine("El arreglo es:");
foreach (var numero in numeros)
{
Console.Write(numero + ",");
}
Console.WriteLine("");
// Ahora sí, buscar de manera binaria
int busqueda = 11;
int indice = busquedaBinaria(numeros, busqueda, 0, numeros.Length - 1);
// Con while sería:
// int indice = busquedaBinariaWhile(numeros, busqueda);
if (indice == -1)
{
Console.WriteLine("La búsqueda no existe");
}
else
{
Console.WriteLine("El elemento {0} existe en la posición {1}", busqueda, indice);
}
}
}
}Si C sharp o C# te gusta, te invito a leer más entradas sobre este lenguaje en mi blog.
