Hoy toca ver una estructura de datos en Java: el árbol binario. Vamos a crear una clase para gestionar un árbol binario que tendrá las siguientes características:
- Insertar datos (de manera balanceada)
- Buscar datos
- Recorrer en preorden, inorden y postorden
Además de eso, nuestro árbol tendrá soporte para datos de tipo String y de tipo int, por lo que podremos almacenar, buscar y mostrar datos tanto de cadena como de tipo entero.
Clase Nodo
Los árboles tienen nodos u hojas. Cada nodo tiene: un dato, un Nodo izquierdo y uno derecho. A su vez cada Nodo hijo puede tener más nodos y así hasta formar un árbol.
He implementado la siguiente clase en Java:
class Nodo {
private int dato;
private Nodo izquierda, derecha;
public Nodo(int dato) {
this.dato = dato;
this.izquierda = this.derecha = null;
}
public int getDato() {
return dato;
}
public Nodo getIzquierda() {
return izquierda;
}
public void setIzquierda(Nodo izquierda) {
this.izquierda = izquierda;
}
public Nodo getDerecha() {
return derecha;
}
public void setDerecha(Nodo derecha) {
this.derecha = derecha;
}
public void imprimirDato() {
System.out.println(this.getDato());
}
}
Lo único que tienes es una referencia a un Nodo izquierda y a otro nodo derecha (ambos pueden ser nulos o tener a su vez otro izquierda y/o derecha). Además de los getters, setters y finalmente el dato que guarda cada nodo.
El árbol
Vamos a crear una clase llamada Arbol que gestionará los Nodos. Esto es para abstraer más fácil todo esto de los árboles binarios en Java.
Método insertar
Esta función se encarga de insertar el valor dependiendo del mismo. Se hace lo siguiente: si la raíz no tiene dato, se le asigna el valor. En caso de que la raíz ya tenga un dato, se comprueba si el dato es menor, y si es así, se asigna al nodo izquierda de la raíz.
Si el dato es mayor que el dato de la raíz, entonces se coloca en la derecha de la raíz.
Pero además: si ya hay un dato a la izquierda o derecha de la raíz, se comprueba la izquierda o derecha del mismo de manera recursiva. Es decir, conforme el árbol crezca, se recorrerán más hojas para colocar de manera efectiva el nodo.
Si te fijas es un método sobrecargado. El que existe de forma simplemente recibe un dato que se insertará sin que el invocador tenga que acomodarlo.
En cambio el método privado recibe el nodo en el que se inserta, y busca la mejor manera de acomodarlo usando recursividad (línea 9 a 23).
Recorridos del árbol
Para los árboles binarios existen 3 tipos de recorridos: preorden, postorden e inorden. Vamos a ver los tres:
private void preorden(Nodo n) {
if (n != null) {
n.imprimirDato();
preorden(n.getIzquierda());
preorden(n.getDerecha());
}
}
private void inorden(Nodo n) {
if (n != null) {
inorden(n.getIzquierda());
n.imprimirDato();
inorden(n.getDerecha());
}
}
private void postorden(Nodo n) {
if (n != null) {
postorden(n.getIzquierda());
postorden(n.getDerecha());
n.imprimirDato();
}
}
public void preorden() {
this.preorden(this.raiz);
}
public void inorden() {
this.inorden(this.raiz);
}
public void postorden() {
this.postorden(this.raiz);
}Como puedes ver lo único que cambia en los 3 métodos es el órden de visita de cada nodo. En uno primero se visita el actual, luego el izquierdo y luego el derecho.
En el inorden primero se visitan todos los nodos izquierda, luego el central y finalmente el de la derecha.
El recorrido postorden primero recorre la izquierda, luego la derecha y finalmente el nodo actual.
Lo interesante aquí es que, al recorrer el árbol inorden se obtendrán los datos ordenados.
Búsqueda dentro del árbol
Un método común requerido en los árboles es la búsqueda. En este caso vamos a crear una función que indica si determinado dato existe o no dentro del árbol.
La magia de todo esto es que la búsqueda será muy rápida, pues los datos están ordenados (los menores a la raíz están a la izquierda; los mayores a la derecha) así que digamos que se hará una búsqueda binaria.
public boolean existe(int busqueda) {
return existe(this.raiz, busqueda);
}
private boolean existe(Nodo n, int busqueda) {
if (n == null) {
return false;
}
if (n.getDato() == busqueda) {
return true;
} else if (busqueda < n.getDato()) {
return existe(n.getIzquierda(), busqueda);
} else {
return existe(n.getDerecha(), busqueda);
}
Como puedes ver igualmente existen dos métodos, uno que es el que se invoca desde la clase y otro que se invoca internamente. Se usa de igual modo la recursión para seguir buscando por todos los nodos.
La recursión se detiene bien cuando se encuentra el valor o cuando ya no quedan nodos por recorrer.
Creando árbol e insertando datos
Veamos un ejemplo de cómo usar el árbol para insertar datos, recorrerlo y comprobar si un elemento existe dentro.
Arbol arbol = new Arbol();
arbol.insertar(1);
arbol.insertar(2);
arbol.insertar(3);
arbol.insertar(4);
arbol.insertar(0);
System.out.println("Recorriendo inorden:");
arbol.inorden();
System.out.println("Recorriendo postorden:");
arbol.postorden();
System.out.println("Recorriendo preorden:");
arbol.preorden();
System.out.println(arbol.existe(1)); // true
System.out.println(arbol.existe(7)); // false
System.out.println(arbol.existe(0)); // trueCódigo completo
Ahora veamos el código completo que conforma todo este ejercicio. Queda así:
/*
____ _____ _ _ _
| _ \ | __ \ (_) | | |
| |_) |_ _ | |__) |_ _ _ __ _____| |__ _ _| |_ ___
| _ <| | | | | ___/ _` | '__|_ / | '_ \| | | | __/ _ \
| |_) | |_| | | | | (_| | | / /| | |_) | |_| | || __/
|____/ \__, | |_| \__,_|_| /___|_|_.__/ \__, |\__\___|
__/ | __/ |
|___/ |___/
Blog: https://parzibyte.me/blog
Ayuda: https://parzibyte.me/blog/contrataciones-ayuda/
Contacto: https://parzibyte.me/blog/contacto/
Copyright (c) 2020 Luis Cabrera Benito
Licenciado bajo la licencia MIT
El texto de arriba debe ser incluido en cualquier redistribución
* */
class Nodo {
private int dato;
private Nodo izquierda, derecha;
public Nodo(int dato) {
this.dato = dato;
this.izquierda = this.derecha = null;
}
public int getDato() {
return dato;
}
public Nodo getIzquierda() {
return izquierda;
}
public void setIzquierda(Nodo izquierda) {
this.izquierda = izquierda;
}
public Nodo getDerecha() {
return derecha;
}
public void setDerecha(Nodo derecha) {
this.derecha = derecha;
}
public void imprimirDato() {
System.out.println(this.getDato());
}
}
class Arbol {
private Nodo raiz;
public Arbol() {
}
public boolean existe(int busqueda) {
return existe(this.raiz, busqueda);
}
private boolean existe(Nodo n, int busqueda) {
if (n == null) {
return false;
}
if (n.getDato() == busqueda) {
return true;
} else if (busqueda < n.getDato()) {
return existe(n.getIzquierda(), busqueda);
} else {
return existe(n.getDerecha(), busqueda);
}
}
public void insertar(int dato) {
if (this.raiz == null) {
this.raiz = new Nodo(dato);
} else {
this.insertar(this.raiz, dato);
}
}
private void insertar(Nodo padre, int dato) {
if (dato > padre.getDato()) {
if (padre.getDerecha() == null) {
padre.setDerecha(new Nodo(dato));
} else {
this.insertar(padre.getDerecha(), dato);
}
} else {
if (padre.getIzquierda() == null) {
padre.setIzquierda(new Nodo(dato));
} else {
this.insertar(padre.getIzquierda(), dato);
}
}
}
private void preorden(Nodo n) {
if (n != null) {
n.imprimirDato();
preorden(n.getIzquierda());
preorden(n.getDerecha());
}
}
private void inorden(Nodo n) {
if (n != null) {
inorden(n.getIzquierda());
n.imprimirDato();
inorden(n.getDerecha());
}
}
private void postorden(Nodo n) {
if (n != null) {
postorden(n.getIzquierda());
postorden(n.getDerecha());
n.imprimirDato();
}
}
public void preorden() {
this.preorden(this.raiz);
}
public void inorden() {
this.inorden(this.raiz);
}
public void postorden() {
this.postorden(this.raiz);
}
}
class Main {
public static void main(String[] argumentos) {
Arbol arbol = new Arbol();
arbol.insertar(1);
arbol.insertar(2);
arbol.insertar(3);
arbol.insertar(4);
arbol.insertar(0);
System.out.println("Recorriendo inorden:");
arbol.inorden();
System.out.println("Recorriendo postorden:");
arbol.postorden();
System.out.println("Recorriendo preorden:");
arbol.preorden();
System.out.println(arbol.existe(1)); // true
System.out.println(arbol.existe(7)); // false
System.out.println(arbol.existe(0)); // true
}
}Árbol binario con nodo String
Como lo prometí al inicio, también dejo un ejemplo de árbol binario en Java pero ahora con Nodos/Hojas cuyo dato es de tipo String.
No es nada complejo, solo cambia la forma de comparar, pues usamos compareTo y equals para saber si una cadena es “menor o mayor” que otra.
class NodoCadena {
private String dato;
private NodoCadena izquierda, derecha;
public NodoCadena(String dato) {
this.dato = dato;
this.izquierda = this.derecha = null;
}
public String getDato() {
return dato;
}
public NodoCadena getIzquierda() {
return izquierda;
}
public void setIzquierda(NodoCadena izquierda) {
this.izquierda = izquierda;
}
public NodoCadena getDerecha() {
return derecha;
}
public void setDerecha(NodoCadena derecha) {
this.derecha = derecha;
}
public void imprimirDato() {
System.out.println(this.getDato());
}
}
class ArbolCadenas {
private NodoCadena raiz;
public ArbolCadenas() {
}
public boolean existe(String busqueda) {
return existe(this.raiz, busqueda);
}
private boolean existe(NodoCadena n, String busqueda) {
if (n == null) {
return false;
}
if (n.getDato().equals(busqueda)) {
return true;
} else if (busqueda.compareTo(n.getDato()) < 0) {
return existe(n.getIzquierda(), busqueda);
} else {
return existe(n.getDerecha(), busqueda);
}
}
public void insertar(String dato) {
if (this.raiz == null) {
this.raiz = new NodoCadena(dato);
} else {
this.insertar(this.raiz, dato);
}
}
private void insertar(NodoCadena padre, String dato) {
if (dato.compareTo(padre.getDato()) > 0) {
if (padre.getDerecha() == null) {
padre.setDerecha(new NodoCadena(dato));
} else {
this.insertar(padre.getDerecha(), dato);
}
} else {
if (padre.getIzquierda() == null) {
padre.setIzquierda(new NodoCadena(dato));
} else {
this.insertar(padre.getIzquierda(), dato);
}
}
}
private void preorden(NodoCadena n) {
if (n != null) {
n.imprimirDato();
preorden(n.getIzquierda());
preorden(n.getDerecha());
}
}
private void inorden(NodoCadena n) {
if (n != null) {
inorden(n.getIzquierda());
n.imprimirDato();
inorden(n.getDerecha());
}
}
private void postorden(NodoCadena n) {
if (n != null) {
postorden(n.getIzquierda());
postorden(n.getDerecha());
n.imprimirDato();
}
}
public void preorden() {
this.preorden(this.raiz);
}
public void inorden() {
this.inorden(this.raiz);
}
public void postorden() {
this.postorden(this.raiz);
}
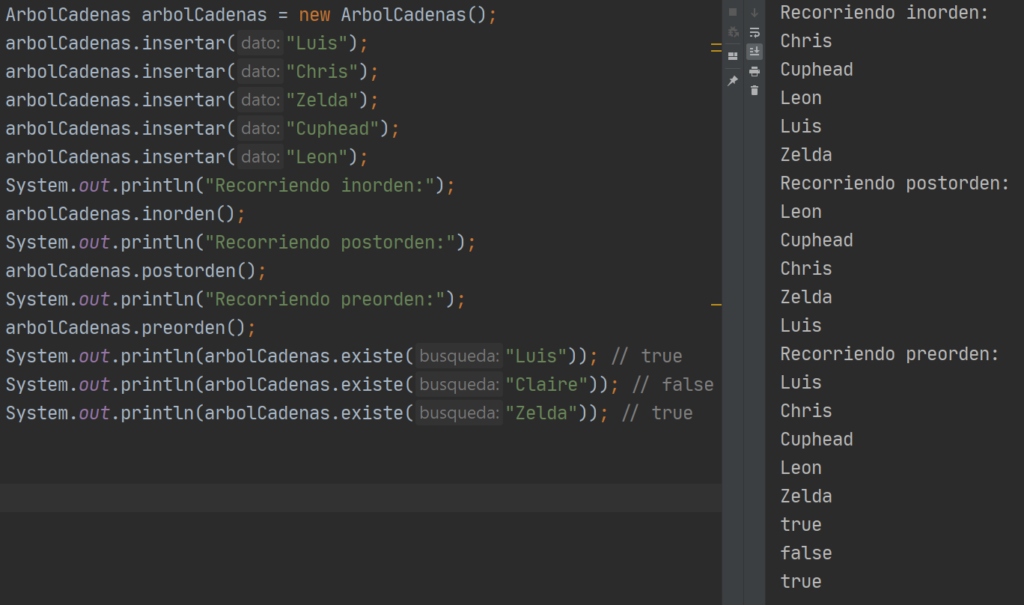
}Su uso es igual al árbol de enteros:
ArbolCadenas arbolCadenas = new ArbolCadenas();
arbolCadenas.insertar("Luis");
arbolCadenas.insertar("Chris");
arbolCadenas.insertar("Zelda");
arbolCadenas.insertar("Cuphead");
arbolCadenas.insertar("Leon");
System.out.println("Recorriendo inorden:");
arbolCadenas.inorden();
System.out.println("Recorriendo postorden:");
arbolCadenas.postorden();
System.out.println("Recorriendo preorden:");
arbolCadenas.preorden();
System.out.println(arbolCadenas.existe("Luis")); // true
System.out.println(arbolCadenas.existe("Claire")); // false
System.out.println(arbolCadenas.existe("Zelda")); // truePoniendo todo junto
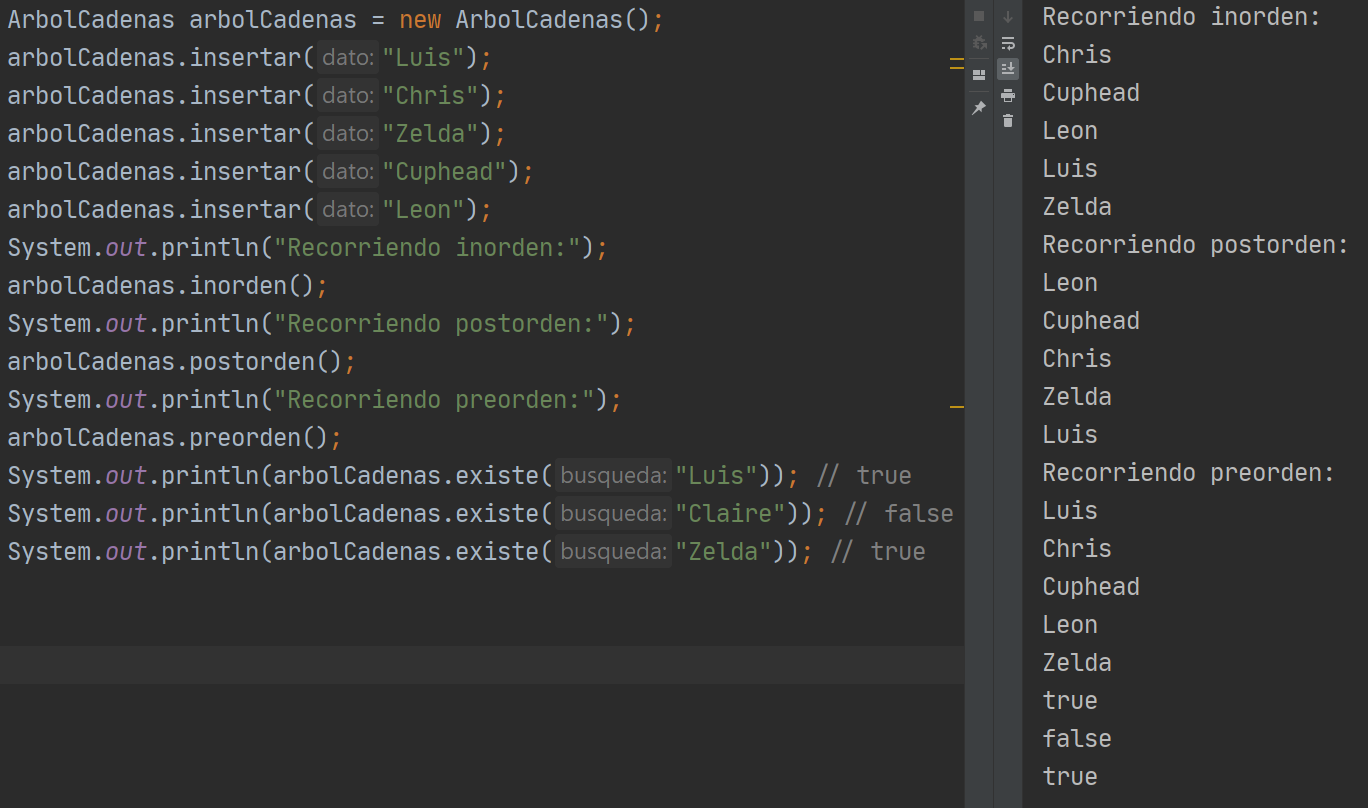
Las dos clases de árboles y sus respectivos nodos así como el modo de uso se engloban en el siguiente archivo:
/*
____ _____ _ _ _
| _ \ | __ \ (_) | | |
| |_) |_ _ | |__) |_ _ _ __ _____| |__ _ _| |_ ___
| _ <| | | | | ___/ _` | '__|_ / | '_ \| | | | __/ _ \
| |_) | |_| | | | | (_| | | / /| | |_) | |_| | || __/
|____/ \__, | |_| \__,_|_| /___|_|_.__/ \__, |\__\___|
__/ | __/ |
|___/ |___/
Blog: https://parzibyte.me/blog
Ayuda: https://parzibyte.me/blog/contrataciones-ayuda/
Contacto: https://parzibyte.me/blog/contacto/
Copyright (c) 2020 Luis Cabrera Benito
Licenciado bajo la licencia MIT
El texto de arriba debe ser incluido en cualquier redistribución
* */
package me.parzibyte;
import java.util.TreeMap;
class NodoCadena {
private String dato;
private NodoCadena izquierda, derecha;
public NodoCadena(String dato) {
this.dato = dato;
this.izquierda = this.derecha = null;
}
public String getDato() {
return dato;
}
public NodoCadena getIzquierda() {
return izquierda;
}
public void setIzquierda(NodoCadena izquierda) {
this.izquierda = izquierda;
}
public NodoCadena getDerecha() {
return derecha;
}
public void setDerecha(NodoCadena derecha) {
this.derecha = derecha;
}
public void imprimirDato() {
System.out.println(this.getDato());
}
}
class ArbolCadenas {
private NodoCadena raiz;
public ArbolCadenas() {
}
public boolean existe(String busqueda) {
return existe(this.raiz, busqueda);
}
private boolean existe(NodoCadena n, String busqueda) {
if (n == null) {
return false;
}
if (n.getDato().equals(busqueda)) {
return true;
} else if (busqueda.compareTo(n.getDato()) < 0) {
return existe(n.getIzquierda(), busqueda);
} else {
return existe(n.getDerecha(), busqueda);
}
}
public void insertar(String dato) {
if (this.raiz == null) {
this.raiz = new NodoCadena(dato);
} else {
this.insertar(this.raiz, dato);
}
}
private void insertar(NodoCadena padre, String dato) {
if (dato.compareTo(padre.getDato()) > 0) {
if (padre.getDerecha() == null) {
padre.setDerecha(new NodoCadena(dato));
} else {
this.insertar(padre.getDerecha(), dato);
}
} else {
if (padre.getIzquierda() == null) {
padre.setIzquierda(new NodoCadena(dato));
} else {
this.insertar(padre.getIzquierda(), dato);
}
}
}
private void preorden(NodoCadena n) {
if (n != null) {
n.imprimirDato();
preorden(n.getIzquierda());
preorden(n.getDerecha());
}
}
private void inorden(NodoCadena n) {
if (n != null) {
inorden(n.getIzquierda());
n.imprimirDato();
inorden(n.getDerecha());
}
}
private void postorden(NodoCadena n) {
if (n != null) {
postorden(n.getIzquierda());
postorden(n.getDerecha());
n.imprimirDato();
}
}
public void preorden() {
this.preorden(this.raiz);
}
public void inorden() {
this.inorden(this.raiz);
}
public void postorden() {
this.postorden(this.raiz);
}
}
class Nodo {
private int dato;
private Nodo izquierda, derecha;
public Nodo(int dato) {
this.dato = dato;
this.izquierda = this.derecha = null;
}
public int getDato() {
return dato;
}
public Nodo getIzquierda() {
return izquierda;
}
public void setIzquierda(Nodo izquierda) {
this.izquierda = izquierda;
}
public Nodo getDerecha() {
return derecha;
}
public void setDerecha(Nodo derecha) {
this.derecha = derecha;
}
public void imprimirDato() {
System.out.println(this.getDato());
}
}
class Arbol {
private Nodo raiz;
public Arbol() {
}
public boolean existe(int busqueda) {
return existe(this.raiz, busqueda);
}
private boolean existe(Nodo n, int busqueda) {
if (n == null) {
return false;
}
if (n.getDato() == busqueda) {
return true;
} else if (busqueda < n.getDato()) {
return existe(n.getIzquierda(), busqueda);
} else {
return existe(n.getDerecha(), busqueda);
}
}
public void insertar(int dato) {
if (this.raiz == null) {
this.raiz = new Nodo(dato);
} else {
this.insertar(this.raiz, dato);
}
}
private void insertar(Nodo padre, int dato) {
if (dato > padre.getDato()) {
if (padre.getDerecha() == null) {
padre.setDerecha(new Nodo(dato));
} else {
this.insertar(padre.getDerecha(), dato);
}
} else {
if (padre.getIzquierda() == null) {
padre.setIzquierda(new Nodo(dato));
} else {
this.insertar(padre.getIzquierda(), dato);
}
}
}
private void preorden(Nodo n) {
if (n != null) {
n.imprimirDato();
preorden(n.getIzquierda());
preorden(n.getDerecha());
}
}
private void inorden(Nodo n) {
if (n != null) {
inorden(n.getIzquierda());
n.imprimirDato();
inorden(n.getDerecha());
}
}
private void postorden(Nodo n) {
if (n != null) {
postorden(n.getIzquierda());
postorden(n.getDerecha());
n.imprimirDato();
}
}
public void preorden() {
this.preorden(this.raiz);
}
public void inorden() {
this.inorden(this.raiz);
}
public void postorden() {
this.postorden(this.raiz);
}
}
public class Main {
public static void main(String[] argumentos) {
Arbol arbol = new Arbol();
arbol.insertar(1);
arbol.insertar(2);
arbol.insertar(3);
arbol.insertar(4);
arbol.insertar(0);
System.out.println("Recorriendo inorden:");
arbol.inorden();
System.out.println("Recorriendo postorden:");
arbol.postorden();
System.out.println("Recorriendo preorden:");
arbol.preorden();
System.out.println(arbol.existe(1)); // true
System.out.println(arbol.existe(7)); // false
System.out.println(arbol.existe(0)); // true
ArbolCadenas arbolCadenas = new ArbolCadenas();
arbolCadenas.insertar("Luis");
arbolCadenas.insertar("Chris");
arbolCadenas.insertar("Zelda");
arbolCadenas.insertar("Cuphead");
arbolCadenas.insertar("Leon");
System.out.println("Recorriendo inorden:");
arbolCadenas.inorden();
System.out.println("Recorriendo postorden:");
arbolCadenas.postorden();
System.out.println("Recorriendo preorden:");
arbolCadenas.preorden();
System.out.println(arbolCadenas.existe("Luis")); // true
System.out.println(arbolCadenas.existe("Claire")); // false
System.out.println(arbolCadenas.existe("Zelda")); // true
}
}
Pequeña nota sobre los genéricos
Si te fijas en los ejemplos anteriores puedes ver que tuvimos que implementar un Nodo para cada tipo de dato, pero gracias a los genéricos se podría implementar un Nodo genérico cuyo tipo de dato fuera cualquiera.
Para ello se me ocurre implementar una interfaz que exponga dos métodos: compareTo y equals, así como las cadenas (pero con otros tipos de datos). De este modo podríamos tener árboles de todo tipo.
Ejemplo en YouTube
Si quieres puedes ver una explicación en mi canal de YouTube:
Conclusión
El árbol binario es una maravilla, lo que más me gusta es su modo de ordenar los datos de manera que queden, valga la redundancia, ordenados.
Te invito a ver un ejemplo de árbol binario en C.
Que tal bro, disculpa como se guardaría la información que se ingresan en los nodos.
Pd: Estoy realizando un adivinar animales pero me gustaría que esta información que se ingresa quede almacenada para cuando yo quiera volver a ejecutar el programa en java. De antemano te agradecería mucho, saludos.
Hola. Gracias por sus comentarios. Si tiene alguna consulta, solicitud de creación de un programa o solicitud de cambio de software estoy para servirle en https://parzibyte.me/#contacto
Saludos!