Quicksort en Java para ordenar arreglos

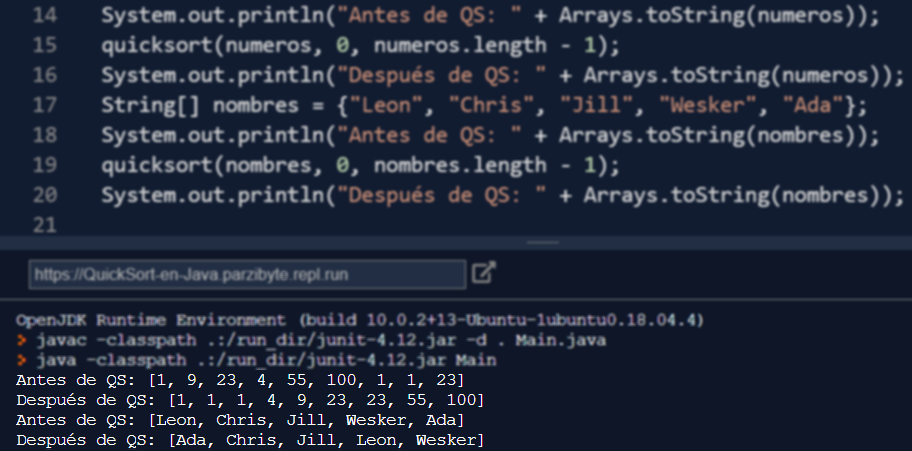
Quicksort en Java - Ejecución del método para ordenar arreglos
Resumen: implementar QuickSort en Java usando recursividad, selección de pivote y principio divide y vencerás para ordenar arreglos, ya sea de tipo int o de tipo String.
QuickSort en Java
Este algoritmo es uno de los más rápidos al momento de ordenar arreglos, en comparación con el ordenamiento de burbuja.
Así como es más rápido, es un poco complejo de entender, pero básicamente se trata de dos cosas:
Partición o pivote
Primero debemos encontrar la partición del arreglo, comenzamos un ciclo infinito y apuntamos dos variables al inicio y final del arreglo. Mientras cada elemento en el índice de cada variable esté en orden, acercamos las variables entre sí, es decir, aumentamos izquierda y disminuimos derecha.
Si la izquierda superó o igualó a la derecha, significa que los elementos ya estaban en orden así que regresamos el índice de la derecha para que de ahí se divida el arreglo, y termina el ciclo.
En caso de que la izquierda no haya superado a la derecha significa que por ahí había un elemento desordenado, por lo que intercambiamos las variables de cada extremo y el ciclo se sigue ejecutando.
Quicksort
La partición es lo que realmente ordena el arreglo e indica de dónde partir para dividir el arreglo. Entonces en el quicksort invocamos a particion para saber cómo dividir el arreglo (es decir, desde cuál índice) e invocamos a quicksort dos veces con cada mitad del arreglo.
Código Java para arreglo de enteros
Veamos el código que va a generar todo esto. Primero vemos el de la partición, que es el que ordena y selecciona desde dónde dividir el arreglo:
private static int particion(int arreglo[], int izquierda, int derecha) {
int pivote = arreglo[izquierda];
// Ciclo infinito
while (true) {
while (arreglo[izquierda] < pivote) {
izquierda++;
}
while (arreglo[derecha] > pivote) {
derecha--;
}
if (izquierda >= derecha) {
return derecha;
} else {//Nota: yo sé que el else no hace falta por el return de arriba, pero así el algoritmo es más claro
int temporal = arreglo[izquierda];
arreglo[izquierda] = arreglo[derecha];
arreglo[derecha] = temporal;
izquierda++;
derecha--;
}
// El while se repite hasta que izquierda >= derecha
}
}
Es realmente sencillo, y al final regresamos el índice en donde se va a dividir el arreglo. Después, en la implementación, usamos recursión como lo dije:
// Divide y vencerás
private static void quicksort(int arreglo[], int izquierda, int derecha) {
if (izquierda < derecha) {
int indiceParticion = particion(arreglo, izquierda, derecha);
quicksort(arreglo, izquierda, indiceParticion);
quicksort(arreglo, indiceParticion + 1, derecha);
}
}La función recibe el arreglo, el inicio y el fin. Después utiliza esos elementos para obtener el índice para dividir, y envía las dos mitades a ordenarse.
La función no regresa nada porque ordena el arreglo internamente.
Así que al invocarla por primera vez debemos pasar el arreglo, el 0 y la longitud - 1.
Quicksort en Java para arreglos de cadena o String
Ahora veamos cómo ordenar un arreglo de cadena usando QuickSort. Esto es igualmente fácil y el código casi no cambia, pues usamos compareTo para comparar cadenas en Java.
El algoritmo es el mismo, solo cambia la comparación por lo que no explicaré el método. La selección del pivote y la función quicksort queda así (presta atención a la línea 12):
private static int particion(String arreglo[], int izquierda, int derecha) {
// Elegimos el pivote, es el primero
String pivote = arreglo[izquierda];
// Ciclo infinito
while (true) {
// Mientras cada elemento desde la izquierda esté en orden (sea menor que el
// pivote) continúa avanzando el índice
while (arreglo[izquierda].compareTo(pivote) < 0) {
izquierda++;
}
// Mientras cada elemento desde la derecha esté en orden (sea mayor que el
// pivote) continúa disminuyendo el índice
while (arreglo[derecha].compareTo(pivote) > 0) {
derecha--;
}
/*
Si la izquierda es mayor o igual que la derecha significa que no
necesitamos hacer ningún intercambio
de variables, pues los elementos ya están en orden (al menos en esta
iteración)
*/ if (izquierda >= derecha) {
// Indicar "en dónde nos quedamos" para poder dividir el arreglo de nuevo
// y ordenar los demás elementos
return derecha;
} else {//Nota: yo sé que el else no hace falta por el return de arriba, pero así el algoritmo es más claro
/*
Si las variables quedaron "lejos" (es decir, la izquierda no superó ni
alcanzó a la derecha)
significa que se detuvieron porque encontraron un valor que no estaba
en orden, así que lo intercambiamos
*/ String temporal = arreglo[izquierda];
arreglo[izquierda] = arreglo[derecha];
arreglo[derecha] = temporal;
/*
Ya intercambiamos, pero seguimos avanzando los índices una vez más
*/ izquierda++;
derecha--;
}
// El while se repite hasta que izquierda >= derecha
}
}
// Divide y vencerás
private static void quicksort(String arreglo[], int izquierda, int derecha) {
if (izquierda < derecha) {
int indiceParticion = particion(arreglo, izquierda, derecha);
quicksort(arreglo, izquierda, indiceParticion);
quicksort(arreglo, indiceParticion + 1, derecha);
}
}
Si te molestan los comentarios puedes removerlos, al final el código es realmente poco, lo complejo es entenderlo de manera humana.
Poniendo todo junto
Ahora voy a demostrar que lo expuesto realmente funciona; veamos cómo probar los métodos. Queda así:
/*
* Archivo: QuickSort.java
* Clase: QuickSort
* Autor: parzibyte
* Fecha: 12/26/19 4:07 PM
* Visita https://parzibyte.me/blog para más tutoriales sobre Java
*/
import java.util.Arrays;
public class QuickSort {
public static void main(String[] args) {
int numeros[] = {1, 9, 23, 4, 55, 100, 1, 1, 23};
System.out.println("Antes de QS: " + Arrays.toString(numeros));
quicksort(numeros, 0, numeros.length - 1);
System.out.println("Después de QS: " + Arrays.toString(numeros));
String[] nombres = {"Leon", "Chris", "Jill", "Wesker", "Ada"};
System.out.println("Antes de QS: " + Arrays.toString(nombres));
quicksort(nombres, 0, nombres.length - 1);
System.out.println("Después de QS: " + Arrays.toString(nombres));
}
private static int particion(int arreglo[], int izquierda, int derecha) {
// Elegimos el pivote, es el primero
int pivote = arreglo[izquierda];
// Ciclo infinito
while (true) {
// Mientras cada elemento desde la izquierda esté en orden (sea menor que el
// pivote) continúa avanzando el índice
while (arreglo[izquierda] < pivote) {
izquierda++;
}
// Mientras cada elemento desde la derecha esté en orden (sea mayor que el
// pivote) continúa disminuyendo el índice
while (arreglo[derecha] > pivote) {
derecha--;
}
/*
Si la izquierda es mayor o igual que la derecha significa que no
necesitamos hacer ningún intercambio
de variables, pues los elementos ya están en orden (al menos en esta
iteración)
*/ if (izquierda >= derecha) {
// Indicar "en dónde nos quedamos" para poder dividir el arreglo de nuevo
// y ordenar los demás elementos
return derecha;
} else {//Nota: yo sé que el else no hace falta por el return de arriba, pero así el algoritmo es más claro
/*
Si las variables quedaron "lejos" (es decir, la izquierda no superó ni
alcanzó a la derecha)
significa que se detuvieron porque encontraron un valor que no estaba
en orden, así que lo intercambiamos
*/ int temporal = arreglo[izquierda];
arreglo[izquierda] = arreglo[derecha];
arreglo[derecha] = temporal;
/*
Ya intercambiamos, pero seguimos avanzando los índices una vez más
*/ izquierda++;
derecha--;
}
// El while se repite hasta que izquierda >= derecha
}
}
// Divide y vencerás
private static void quicksort(int arreglo[], int izquierda, int derecha) {
if (izquierda < derecha) {
int indiceParticion = particion(arreglo, izquierda, derecha);
quicksort(arreglo, izquierda, indiceParticion);
quicksort(arreglo, indiceParticion + 1, derecha);
}
}
private static int particion(String arreglo[], int izquierda, int derecha) {
// Elegimos el pivote, es el primero
String pivote = arreglo[izquierda];
// Ciclo infinito
while (true) {
// Mientras cada elemento desde la izquierda esté en orden (sea menor que el
// pivote) continúa avanzando el índice
while (arreglo[izquierda].compareTo(pivote) < 0) {
izquierda++;
}
// Mientras cada elemento desde la derecha esté en orden (sea mayor que el
// pivote) continúa disminuyendo el índice
while (arreglo[derecha].compareTo(pivote) > 0) {
derecha--;
}
/*
Si la izquierda es mayor o igual que la derecha significa que no
necesitamos hacer ningún intercambio
de variables, pues los elementos ya están en orden (al menos en esta
iteración)
*/ if (izquierda >= derecha) {
// Indicar "en dónde nos quedamos" para poder dividir el arreglo de nuevo
// y ordenar los demás elementos
return derecha;
} else {//Nota: yo sé que el else no hace falta por el return de arriba, pero así el algoritmo es más claro
/*
Si las variables quedaron "lejos" (es decir, la izquierda no superó ni
alcanzó a la derecha)
significa que se detuvieron porque encontraron un valor que no estaba
en orden, así que lo intercambiamos
*/ String temporal = arreglo[izquierda];
arreglo[izquierda] = arreglo[derecha];
arreglo[derecha] = temporal;
/*
Ya intercambiamos, pero seguimos avanzando los índices una vez más
*/ izquierda++;
derecha--;
}
// El while se repite hasta que izquierda >= derecha
}
}
// Divide y vencerás
private static void quicksort(String arreglo[], int izquierda, int derecha) {
if (izquierda < derecha) {
int indiceParticion = particion(arreglo, izquierda, derecha);
quicksort(arreglo, izquierda, indiceParticion);
quicksort(arreglo, indiceParticion + 1, derecha);
}
}
}
Estoy usando Arrays.toString para imprimir el arreglo de forma rápida; si tú quieres, puedes imprimirlos con un ciclo o algo así.
La salida de la ejecución del código es:
Te invito a ver el método de la burbuja en Java, el método QuickSort en C o más tutoriales sobre Java.
Entradas recientes
Resetear GOOJPRT PT-210 MTP-II (Impresora térmica)
El día de hoy vamos a ver cómo restablecer la impresora térmica GOOJPRT PT-210 a…
Proxy Android para impresora térmica ESC POS
Hoy voy a enseñarte cómo imprimir en una impresora térmica conectada por USB a una…
Android – Servidor web con servicio en segundo plano
En este post voy a enseñarte a programar un servidor web en Android asegurándonos de…
Cancelar trabajo de impresión con C++
En este post te quiero compartir un código de C++ para listar y cancelar trabajos…
Copiar bytes de Golang a JavaScript con WebAssembly
Gracias a WebAssembly podemos ejecutar código de otros lenguajes de programación desde el navegador web…
Imprimir PDF con Ghostscript en Windows de manera programada
Revisando y buscando maneras de imprimir un PDF desde la línea de comandos me encontré…
Ver comentarios
Jajaja parece que alguien por aqui es fan de Resident Evil xD
Gracias por la información! Está muy clara y bien explicada, me ayudaste muchísimo
Gracias por sus comentarios. Me agrada saber que le haya funcionado.
Saludos!