Introducción

Ya fue el turno de PHP, JavaScript, Java (con strings y números) y Python.

Hoy es el turno de uno de mis lenguajes de programación favoritos: Go. Veremos cómo se puede implementar la búsqueda binaria en los arreglos del lenguaje, tanto en cadenas como en números.

Al igual que en los otros ejercicios, veremos:

• Búsqueda binaria recursiva en arreglos de números
• Búsqueda binaria secuencial en arreglos de números
• Implementación de búsqueda binaria recursiva en arreglos de strings o cadenas
• Algoritmo de búsqueda binaria secuencial en arreglos de cadenas

Ver en línea

He puesto este código en el playground de Go.

Explicación del algoritmo

Bueno, esto ya lo he dicho en los otros posts y te invito a leerlos, pero igualmente trataré de dar la explicación…

Antes de todo, el arreglo debe estar ordenado. Es un requisito; aquí no veremos cómo ordenarlo porque ese no es el tema; veremos cómo hacer la búsqueda binaria. Ten en mente eso porque es importante saberlo para entender el algoritmo.

Este algoritmo utiliza el enfoque de divide y vencerás. Va partiendo el arreglo en 2 cada vez. Por ejemplo, la primera vez tal vez mida 6, luego medirá 3, luego 1 y así. El algoritmo es sencillo:

Calcula el elemento del medio sumando izquierda y derecha, dividiendo entre 2 ese resultado y luego redondeando hacia abajo. Si, por ejemplo, tenemos un arreglo de 5, la primera vez izquierda es 0 y derecha es 4, la mitad es redondearHaciaAbajo((0 + 4) / 2) que es igual a 2. Si fuera de 6, sería redondearHaciaAbajo((0 + 5) / 2) que daría algo como redondearHaciaAbajo(2.5), lo que resultaría en 2 de nuevo.

Una vez que ya sabemos en dónde está la mitad, obtenemos el valor que se encuentra en esa posición del arreglo. Lo comparamos con la búsqueda y en caso de que sea ese, regresamos el índice y el algoritmo termina.

Pero en caso de que el elemento de la mitad no coincida, se compara lo que buscamos. Debido a que el arreglo está ordenado, si el elemento del medio es mayor a la búsqueda, puede que lo que busquemos esté hacia la izquierda de esa mitad, y si el elemento de la mitad es menor a la búsqueda, tal vez lo que busquemos esté a la derecha.

Hacemos un if, y partimos el arreglo, ya sea desde izquierda hasta la mitad menos uno, o desde la mitad más uno hasta derecha.

En determinado momento encontraremos el elemento a la mitad del arreglo, y si no, entonces izquierda será más grande que derecha; justo ahí indicamos que no se encontró lo que buscamos y devolvemos -1.

Cómo comparar las cadenas

Afortunadamente (y no me esperaba menos de un lenguaje tan bonito) en Go podemos comparar cadenas como comparamos números. Es decir, usamos los operadores >, < y todos esos. Este lenguaje trata a las cadenas lexicográficamente, así que no necesitamos usar algo como compareTo como lo hicimos con Java.

Cabe mencionar que la función Compare sí existe en go, pero incluso ellos recomiendan que no la usemos; que siempre es más rápido y limpio usar los operadores binarios.

Cosas que importar

En las funciones no se ve, pero necesitamos importar la librería (o como se le diga) math. En la implementación usamos funciones de fmt, así que igualmente puedes importarlo.

import (
 "fmt"
 "math"
)

Búsqueda binaria recursiva y secuencial en Go

Vamos a ver todas las implementaciones, que en total son 4. Al final veremos cómo podemos usarlas. El algoritmo es el mismo, sólo que algunas usan while y otras recursividad. Recuerda que la condición de salida es igual para todas: que izquierda sea mayor que derecha.

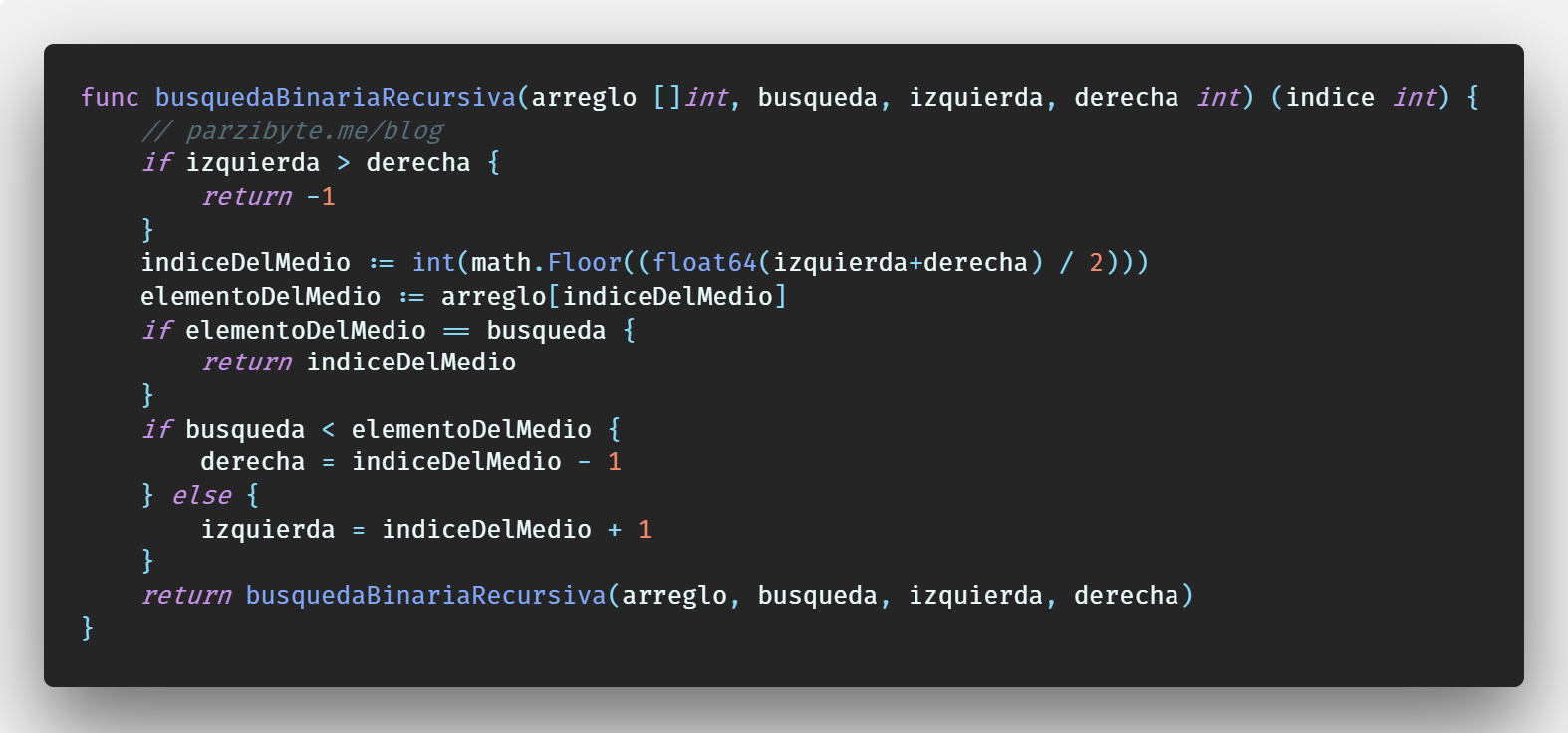
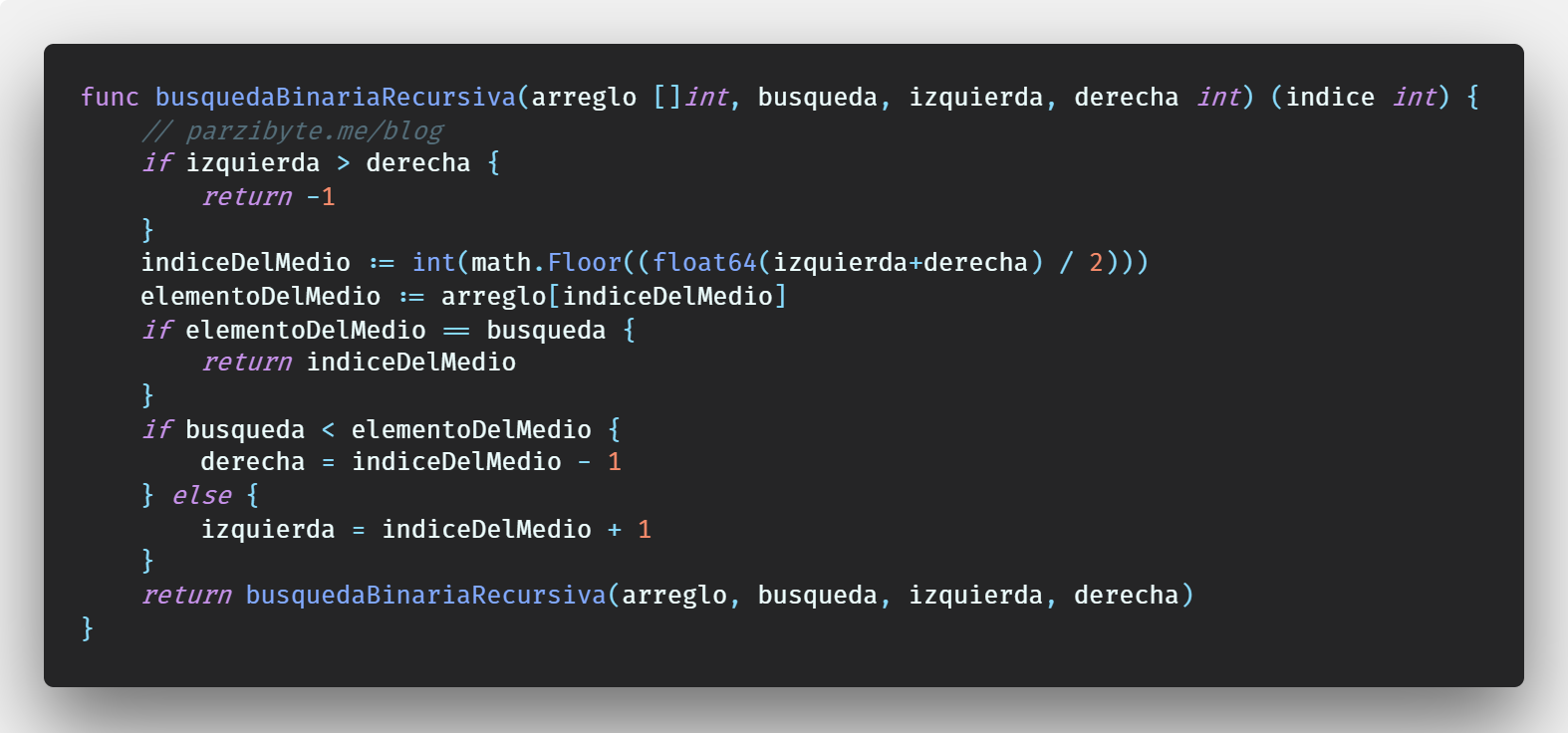
Con arreglos numéricos y recursividad

Comencemos viendo lo más fácil, una búsqueda binaria en un arreglo que tiene números enteros. Aquí el código:

func busquedaBinariaRecursiva(arreglo []int, busqueda, izquierda, derecha int) (indice int) {
 if izquierda > derecha {
  return -1
 }
 indiceDelMedio := int(math.Floor((float64(izquierda+derecha) / 2)))
 elementoDelMedio := arreglo[indiceDelMedio]
 if elementoDelMedio == busqueda {
  return indiceDelMedio
 }
 if busqueda < elementoDelMedio {
  derecha = indiceDelMedio - 1
 } else {
  izquierda = indiceDelMedio + 1
 }
 return busquedaBinariaRecursiva(arreglo, busqueda, izquierda, derecha)
}

Así de sencillo es. Disculpen por todos los casteos que se hacen, pero son necesarios para que el compilador no se queje. Por ejemplo, la función math.Floor recibe un float64, no un int, pero como no somos matemáticos y no nos importa si perdemos precisión, lo casteamos.

Más tarde, convertimos lo que devuelva math.Floor a int, porque devuelve un float64. Esto, si bien se ve sucio, sirve bastante bien porque es mejor que el lenguaje no nos deje perder precisión sin que nosotros lo indiquemos explícitamente cuando estamos trabajando con números grandes o flotantes.

Y si no sabes qué es math.Floor yo te cuento: sirve para redondear números hacia abajo.

Usando arreglos numéricos y while

Lo mismo de arriba pero en un ciclo while. Aunque en Go no existe while, sí existe el ciclo while. Es decir; no existe la palabra reservada, pero podemos hacer el ciclo usando for. Recuerda: For is Go’s “while”

func busquedaBinaria(arreglo []int, busqueda int) (indice int) {
 izquierda := 0
 derecha := len(arreglo) - 1
 
 /*
    Recordemos que For is Go's "while"
    https://tour.golang.org/flowcontrol/3
 */ for izquierda <= derecha {
  indiceDelMedio := int(math.Floor((float64(izquierda+derecha) / 2)))
  elementoDelMedio := arreglo[indiceDelMedio]
  if elementoDelMedio == busqueda {
   return indiceDelMedio
  }
  if busqueda < elementoDelMedio {
   derecha = indiceDelMedio - 1
  } else {
   izquierda = indiceDelMedio + 1
  }
 }
 return -1
}

El algoritmo es el mismo, ya lo dije. Lo que cambia es que la función ahora recibe únicamente el arreglo y la búsqueda, porque la izquierda y la derecha son calculadas internamente y movidas dentro del ciclo while.

Con arreglos de cadenas y de forma recursiva

Ahora veamos el enfoque de comparar cadenas usando recursión. Es igual al numérico, sólo cambian los tipos de datos que recibimos.

func busquedaBinariaCadenas(arreglo []string, busqueda string) (indice int) {
 izquierda := 0
 derecha := len(arreglo) - 1
 /*
    Recordemos que For is Go's "while"
    https://tour.golang.org/flowcontrol/3
 */ for izquierda <= derecha {
  indiceDelMedio := int(math.Floor((float64(izquierda+derecha) / 2)))
  elementoDelMedio := arreglo[indiceDelMedio]
  if elementoDelMedio == busqueda {
   return indiceDelMedio
  }
  if busqueda < elementoDelMedio {
   derecha = indiceDelMedio - 1
  } else {
   izquierda = indiceDelMedio + 1
  }
 }
 return -1
}

No te confundas, el índice del elemento sigue siendo un entero, pero el elemento en sí es un string. Igualmente comparamos a las cadenas con los operadores binarios, así como en los números.

Ciclo while para implementar búsqueda binaria en arreglos de cadenas

El último algoritmo que nos trae aquí es la búsqueda binaria pero de forma secuencial; sobre arreglos de cadenas. Es como el de números, únicamente cambian los tipos de datos.

func busquedaBinariaRecursivaCadenas(arreglo []string, busqueda string, izquierda, derecha int) (indice int) {
 if izquierda > derecha {
  return -1
 }
 indiceDelMedio := int(math.Floor((float64(izquierda+derecha) / 2)))
 elementoDelMedio := arreglo[indiceDelMedio]
 if elementoDelMedio == busqueda {
  return indiceDelMedio
 }
 if busqueda < elementoDelMedio {
  derecha = indiceDelMedio - 1
 } else {
  izquierda = indiceDelMedio + 1
 }
 return busquedaBinariaRecursivaCadenas(arreglo, busqueda, izquierda, derecha)
}

Con eso terminamos los 4 algoritmos que son muy parecidos entre sí. Veamos cómo se implementan.

Probar todas las funciones

He declarado unos arreglos y variables en la función main. Toda la función se ve así:

func main() {
 arregloDeNumeros := []int{1, 2, 3, 4, 5, 5, 6, 7, 8, 9, 9, 10, 12, 15, 18, 20, 21}
 busquedaNumerica := 2
 resultadoBusquedaNumerica := busquedaBinariaRecursiva(arregloDeNumeros, busquedaNumerica, 0, len(arregloDeNumeros)-1)
 fmt.Printf("[Recursivo] Buscando %d en %v... el índice devuelto es %d\n", busquedaNumerica, arregloDeNumeros, resultadoBusquedaNumerica)
 resultadoBusquedaNumerica = busquedaBinaria(arregloDeNumeros, busquedaNumerica)
 fmt.Printf("[Secuencial] Buscando %d en %v... el índice devuelto es %d\n", busquedaNumerica, arregloDeNumeros, resultadoBusquedaNumerica)
 
 arregloCadenas := []string{"Avión", "Barco", "Control", "Linterna", "Teléfono", "Vuelo", "Zapato"}
 busquedaCadena := "Control"
 resultadoBusquedaCadena := busquedaBinariaRecursivaCadenas(arregloCadenas, busquedaCadena, 0, len(arregloCadenas)-1)
 fmt.Printf("[Recursivo] Buscando %s en %v... el índice devuelto es %d\n", busquedaCadena, arregloCadenas, resultadoBusquedaCadena)
 resultadoBusquedaCadena = busquedaBinariaCadenas(arregloCadenas, busquedaCadena)
 fmt.Printf("[Secuencial] Buscando %s en %v... el índice devuelto es %d\n", busquedaCadena, arregloCadenas, resultadoBusquedaCadena)
}

Lo que hace es usar los 4 algoritmos e imprimir los resultados en la consola. Ahora que leo esto, puede que el código sea más rápido si pasamos el arreglo por referencia, sería de probar.

Pero bueno, al ejecutarlo se ve así:

Con eso terminamos.